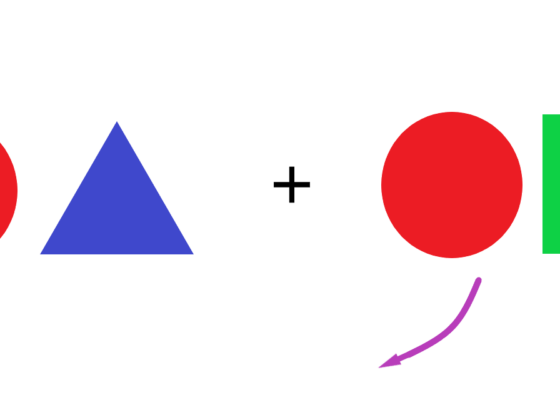
Factoring Expressions Using a Common Factor
https://schooltutoring.com/help/wp-content/uploads/sites/2/2024/03/Factoring.png
1416
672
joshua
https://secure.gravatar.com/avatar/00eceedbde18941838278f3c2f8b0fac6cecb85d72807815021ec4b5a0680ab0?s=96&d=mm&r=g
Learn how to factor algebraic expressions by dividing by a common factor. See how this can be a powerful tool in simplifying expressions. Examples included.
read more
Expanding Algebraic Expressions
https://schooltutoring.com/help/wp-content/uploads/sites/2/2024/02/Expand.png
373
174
joshua
https://secure.gravatar.com/avatar/00eceedbde18941838278f3c2f8b0fac6cecb85d72807815021ec4b5a0680ab0?s=96&d=mm&r=g
Expanding is a powerful tool that allows for the manipulation and simplification of algebraic expressions. Here we will introduce the distribution and foiling expansion methods and show some examples.
read more
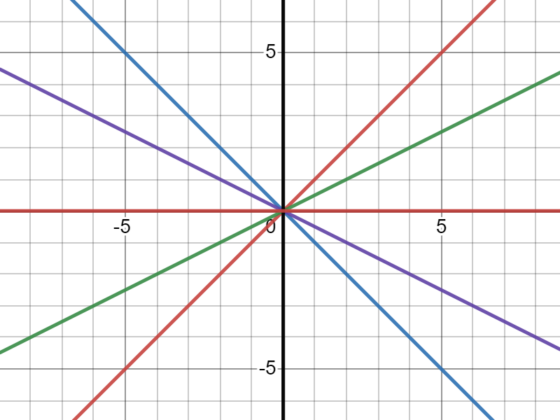
Slope and the slope formula for lines
https://schooltutoring.com/help/wp-content/uploads/sites/2/2024/02/multiple-slopes.png
800
800
Jeff
https://secure.gravatar.com/avatar/da49564a7d5fa4f8d254b73aa7b9ba7a8b6f58d8041af39b9382f3e65d92cee7?s=96&d=mm&r=g
The slope is an essential tool that we use every day. From calculating prices in the supermarket, to cooking we are constantly using it. In this post, we explain the concept of slope and we show some examples of how to calculate it.
read more
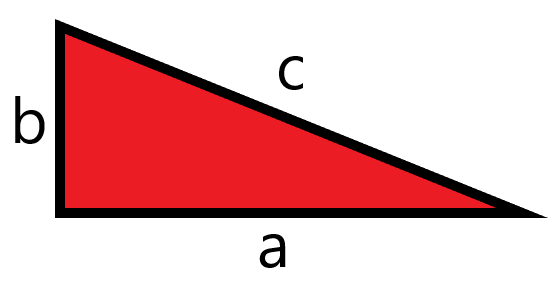
Proving and Using the Pythagorean Theorem
https://schooltutoring.com/help/wp-content/uploads/sites/2/2024/02/Right-Triangle.png
589
281
joshua
https://secure.gravatar.com/avatar/00eceedbde18941838278f3c2f8b0fac6cecb85d72807815021ec4b5a0680ab0?s=96&d=mm&r=g
Here we will look at one of the most important equations in geometry: the Pythagorean Theorem. We will begin by defining the Pythagorean Theorem and then we will demonstrate a short proof. Finally, we will look at two examples of how we might use the the Pythagorean Theorem in a real-world context.
read more
Finding Asymptotes and Holes of Rational Functions
https://schooltutoring.com/help/wp-content/uploads/sites/2/2024/01/1overx-1.png
640
480
joshua
https://secure.gravatar.com/avatar/00eceedbde18941838278f3c2f8b0fac6cecb85d72807815021ec4b5a0680ab0?s=96&d=mm&r=g
Here we will be looking at some defining features of rational functions: asymptotes and holes. We will begin by defining rational functions,. We will then proceed to uncover how to identify different types of asymptotes and how to distinguish them from holes. In each case, we will use example functions to visualize the effects and representations of these features.
read more
Tips for Factoring Polynomials
https://schooltutoring.com/help/wp-content/uploads/sites/2/2019/06/Quintic_polynomial.svg_.png
970
1024
Teaching Staff
https://secure.gravatar.com/avatar/7182184423f0fe174efcd9373374016908ebd464d5461cc3b0f2fe3135131549?s=96&d=mm&r=g
Polynomial Factoring: As in many fields, the manner in which we approach a problem In mathematics can greatly affect how we go about solving it. By finding the factors…
read more
Solving a System of Equations: Substitution and Elimination
https://schooltutoring.com/help/wp-content/uploads/sites/2/2019/01/math-1.jpg
794
629
Teaching Staff
https://secure.gravatar.com/avatar/7182184423f0fe174efcd9373374016908ebd464d5461cc3b0f2fe3135131549?s=96&d=mm&r=g
When dealing with a system of linear equations there are two methods to algebraically solve the question. One is substitution and the other is elimination which is meant to be…
read more
Finding the Equation of a y = mx + b Line
https://schooltutoring.com/help/wp-content/uploads/sites/2/2018/08/lines.jpg
960
490
Teaching Staff
https://secure.gravatar.com/avatar/7182184423f0fe174efcd9373374016908ebd464d5461cc3b0f2fe3135131549?s=96&d=mm&r=g
Math Review of Binomial Distributions
https://schooltutoring.com/help/wp-content/uploads/sites/2/2014/06/Binomial-Distribution-2.jpg
849
565
School Tutoring
https://secure.gravatar.com/avatar/961f85b7fb015cd3d7b4a39357d292c2080323018ae6e327e25442991ed50cc7?s=96&d=mm&r=g
Overview A binomial experiment has a fixed number of independent trials, and each trial has only two possible outcomes. Each of the trials has the same probability of success. The…
read more
Properties of Probability
https://schooltutoring.com/help/wp-content/uploads/sites/2/2014/07/Properties-of-Probability.jpg
500
333
School Tutoring
https://secure.gravatar.com/avatar/961f85b7fb015cd3d7b4a39357d292c2080323018ae6e327e25442991ed50cc7?s=96&d=mm&r=g
Overview: Probability is the measure of the likelihood of an event. The basic mathematics of probability theory started with games of chance, but it can be applied to many situations,…
read more