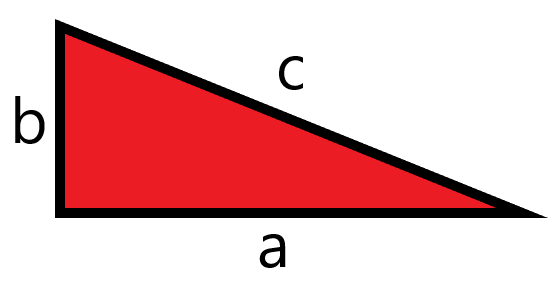
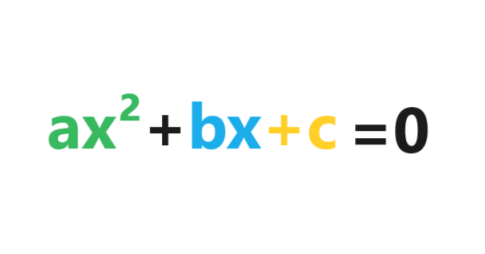What is the Unit Circle and Why is it Important?
https://schooltutoring.com/help/wp-content/uploads/sites/2/2024/03/unit-cicle-1-1.png
600
317
Jeff
https://secure.gravatar.com/avatar/48c4c6cdb7975c0042b502b132288352?s=96&d=mm&r=g
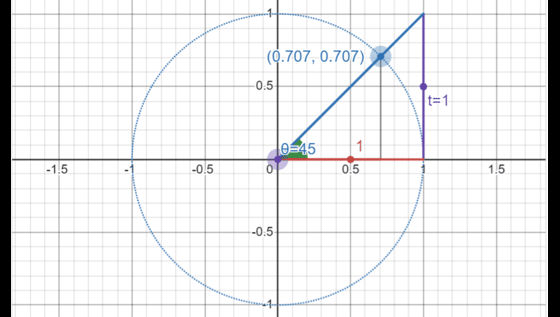
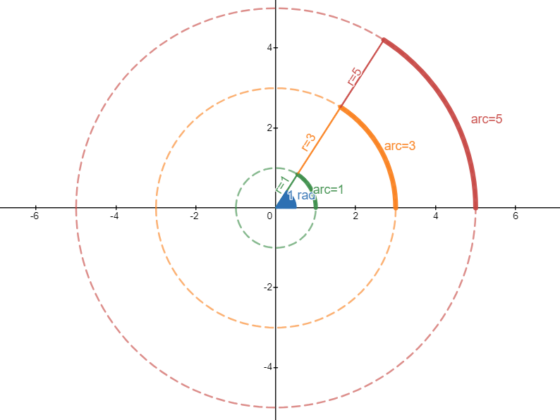
We explore how to use the unit circle to understand some properties of trigonometric ratios and why this circle is so important in math.
read more