Geometry

  • Jeff
  • No Comments

Slope and the slope formula for lines
Slope and the slope formula for lines 800 800 Jeff
The slope is an essential tool that we use every day. From calculating prices in the supermarket, to cooking we are constantly using it. In this post, we explain the concept of slope and we show some examples of how to calculate it. read more
  • joshua
  • No Comments

Proving and Using the Pythagorean Theorem
Proving and Using the Pythagorean Theorem 589 281 joshua
Here we will look at one of the most important equations in geometry: the Pythagorean Theorem. We will begin by defining the Pythagorean Theorem and then we will demonstrate a short proof. Finally, we will look at two examples of how we might use the the Pythagorean Theorem in a real-world context. read more
  • Teaching Staff
  • No Comments

The Pythagorean Theorem
The Pythagorean Theorem 960 664 Teaching Staff

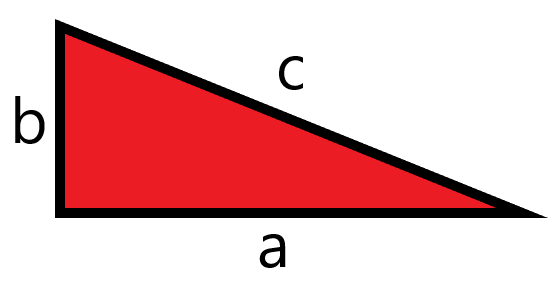
Triangles are an important shape that come up all over the place in life, which is why trigonometry is one of the most important fields of mathematics. Pythagorean theorem is…

read more
  • Teaching Staff
  • No Comments

Sketching Rational Functions
Sketching Rational Functions 630 630 Teaching Staff

Definitions: A rational function is defined as a function where both the numerator and denominator are polynomials.  A hole is a point where the function is undefined. An asymptote is…

read more
  • Teaching Staff
  • No Comments

Basic Angle Properties
Basic Angle Properties 760 446 Teaching Staff

Below are the essential angle properties to have mastered before entering high school. Supplementary Angles: There is 180 degrees in a straight line. Therefore a group of angles that are…

read more
  • Deborah
  • No Comments

Math Review of Representing Solid Figures
Math Review of Representing Solid Figures 150 150 Deborah

Overview Three-dimensional solid figures can be represented by the two-dimensional pattern of polygons that create them. The pattern, called a net, is a visual representation that illustrates the formula for…

read more
  • Deborah
  • No Comments

Math Review of Slopes of Parallel and Perpendicular Lines
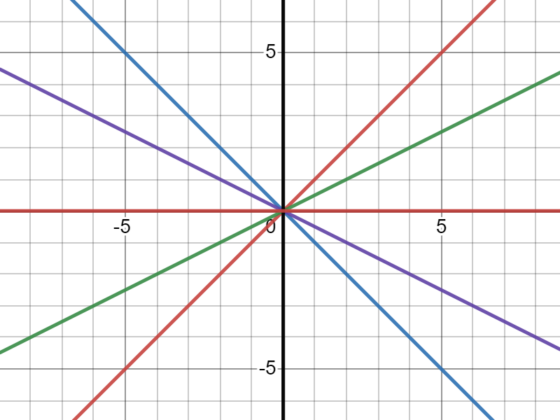
Math Review of Slopes of Parallel and Perpendicular Lines 150 150 Deborah

Overview Lines representing graphs of linear equations have slopes, defined as the change in y/change in x. Parallel lines have the same slope, but no solutions in common. Perpendicular lines…

read more
  • Deborah
  • No Comments

Math and Physics Review of Ice Hockey
Math and Physics Review of Ice Hockey 150 150 Deborah

Overview In the winter sport of ice hockey, players, sticks, and the puck all move at a rapid pace. Sports scientists know that the apparent chaos of the game is…

read more
  • Deborah
  • No Comments

Math and Physics Review of Football
Math and Physics Review of Football 150 150 Deborah

Overview The matchup between NFC West Champion Seattle Seahawks and AFC East Champion New England Patriots promises thrilling gridiron action during Super Bowl XLIX. Behind the scenes, principles of math…

read more
  • Deborah
  • No Comments

Math Review of Volume and Surface Area
Math Review of Volume and Surface Area 150 150 Deborah

Overview Solid objects have both volume and surface area. Formulas for calculations can be expressed using algebra, especially if the measurements of sides are stated by variables. The ratio of…

read more
Enter your
text here