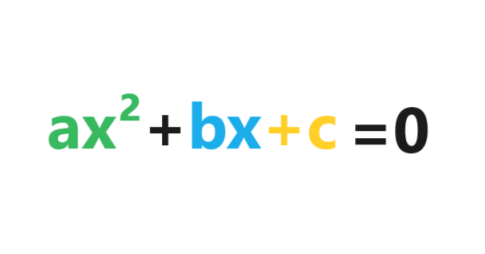Pre-Calculus

The unit circle showing the tangent of an angle as the length of the tangent line in the circle.
  • Jeff
  • No Comments

What is the Unit Circle and Why is it Important?
What is the Unit Circle and Why is it Important? 600 317 Jeff
We explore how to use the unit circle to understand some properties of trigonometric ratios and why this circle is so important in math. read more
The relationship between 1 radian and the radius of a circle
  • Jeff
  • No Comments

What are Radians and Why we Use them
What are Radians and Why we Use them 794 717 Jeff
A radian is the natural unit of angles, but why do we use them instead of degrees. In this post we discuss the relationship between angles, radians and degrees. read more
Quadratic Equation
  • Jeff
  • No Comments

Solving Quadratic Equations
Solving Quadratic Equations 485 254 Jeff
The quadratic equation is one of the most important topics in math, but sometimes it could look a bit complicated. We explore some of the simplest methods to solve quadratic equations and offer some examples of each. read more
  • joshua
  • No Comments

Finding Asymptotes and Holes of Rational Functions
Finding Asymptotes and Holes of Rational Functions 640 480 joshua
Here we will be looking at some defining features of rational functions: asymptotes and holes. We will begin by defining rational functions,. We will then proceed to uncover how to identify different types of asymptotes and how to distinguish them from holes. In each case, we will use example functions to visualize the effects and representations of these features. read more
  • Teaching Staff
  • No Comments

Tips for Factoring Polynomials
Tips for Factoring Polynomials 970 1024 Teaching Staff

Polynomial Factoring:   As in many fields, the manner in which we approach a problem In mathematics can greatly affect how we go about solving it. By finding the factors…

read more
  • Deborah
  • No Comments

The Physics of Spinning Objects
The Physics of Spinning Objects 150 150 Deborah

Overview Any spinning object rotates around a central point called an axis. Tops, dreidels, gyroscopes, and spinning eggs rotate, rise, and seem to defy gravity, as long as they are moving.…

read more
  • Deborah
  • No Comments

Math Review of Leibniz, Newton, and the Development of Calculus
Math Review of Leibniz, Newton, and the Development of Calculus 150 150 Deborah

Overview One of the biggest controversies in science in the early 18th century was around the development of a new mathematical tool called calculus. In Europe, the mathematician, philosopher, and scientist…

read more
  • Deborah
  • No Comments

Math Review of Roulettes and Cycloids
Math Review of Roulettes and Cycloids 150 150 Deborah

Overview Roulettes are special types of curves that are made when one curve is rotated around another by a fixed point. They are in Euclidean space, and can be described…

read more
  • Deborah
  • No Comments

Math Introduction to Infinitesimals
Math Introduction to Infinitesimals 150 150 Deborah

Overview Using infinitesimal quantities to approximate measurement of any item is an ancient way to determine the size and shape of irregular objects. Although it was very controversial in the…

read more
  • Deborah
  • No Comments

Math Introduction to Integrals
Math Introduction to Integrals 150 150 Deborah

Overview Finding integrals, or integration, is the opposite of finding the derivative in calculus. The concept is closely connected with functions, and was independently discussed by both Newton and Leibniz…

read more
Enter your
text here