Naming organic molecules can seem like a daunting task, because lets face it, there are more rules than most of us care to learn. That being said, the aim of…
read morePolynomial Factoring: As in many fields, the manner in which we approach a problem In mathematics can greatly affect how we go about solving it. By finding the factors…
read moreNatural selection is defined as a process or a “force” that allows for organisms better adapted to their environment to better survive and produce more offspring. The theory of natural…
read moreA difficult concept in chemistry is the equilibrium of chemical equations. Chemical reactions do not always react to completion, and they can proceed in either direction if it is written…
read moreLiterary devices are techniques used by writers to create depth and meaning to the messages they are trying to convey. Knowing some of the more common literary devices can be…
read moreTriangles are an important shape that come up all over the place in life, which is why trigonometry is one of the most important fields of mathematics. Pythagorean theorem is…
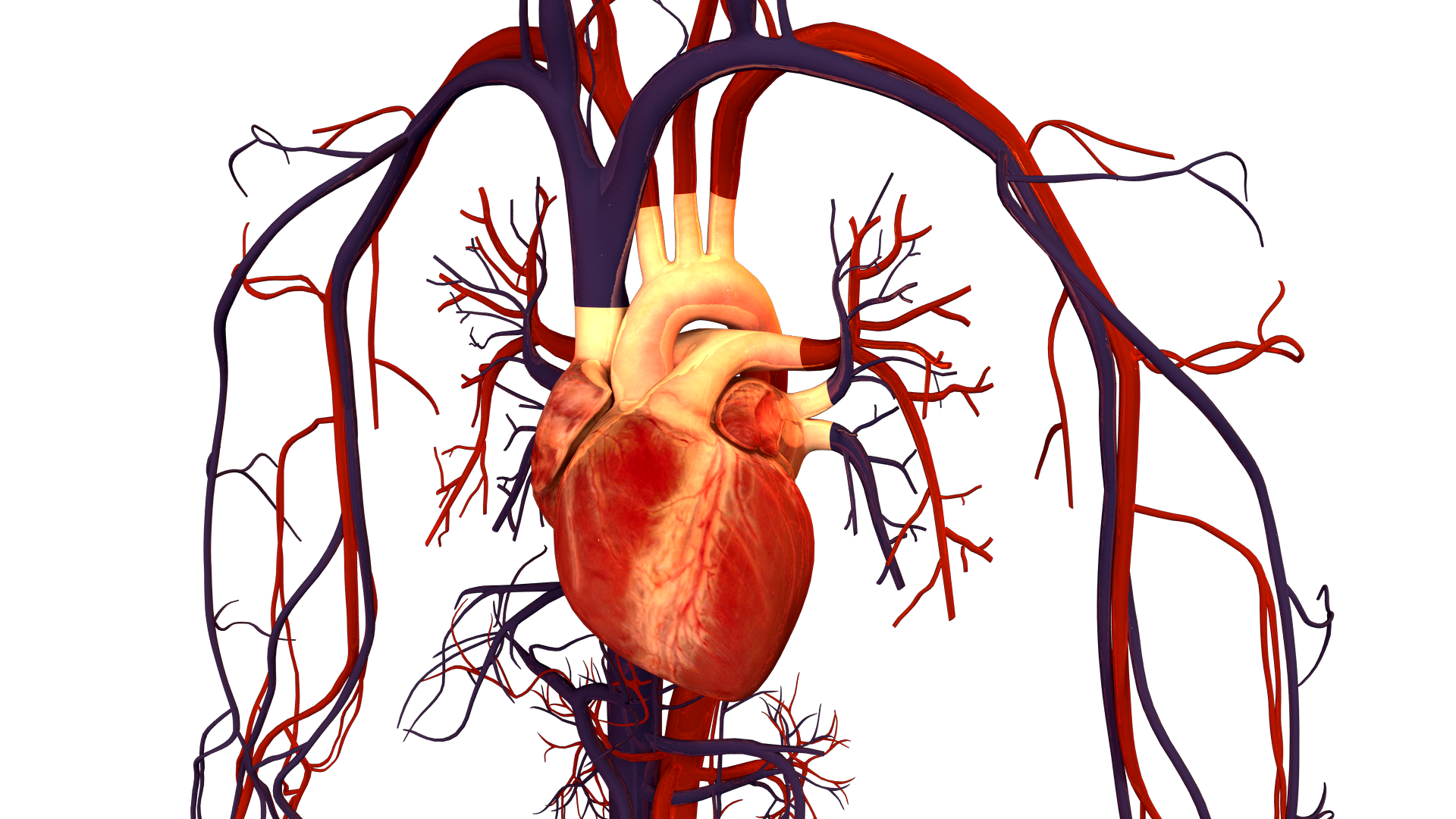
read moreThere are multiple organ systems in the human body that work together to keep us alive. One of these systems is the circulatory system. The major components of the circulatory…
read moreThere are several different types of forces that exist. One way of categorizing different forces is into contact and non-contact forces. A contact force requires something to be physically touching…
read moreThere are various types of chemical reactions that occur in chemistry, but many reactions tend to follow 1 of 5 main types. Becoming familiar with these types of chemical reactions…
read moreThere are several different parts of speech, which are categories of types of words. We are going to talk about four of the main eight parts of speech, which are…
read more