Overview
The AC-method, also known as factoring by grouping, is often used to factor polynomials when the a coefficient is equal to 1. It can also be used when the a coefficient is not equal to 1, similar to the FOIL method.
Questioning the Polynomial Expression
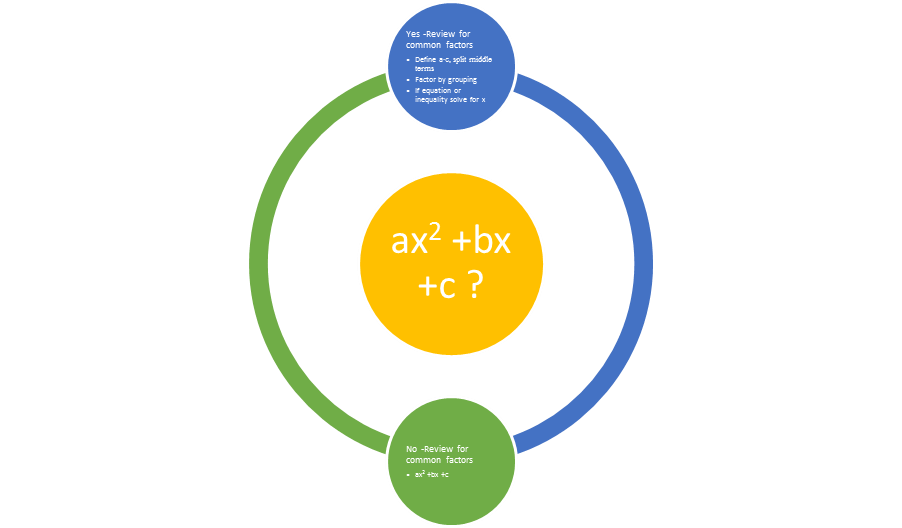
The first step to defining the polynomial expression, before finding factors or a numerical solution, is to see whether or not it takes the form ax2 +bx +c. Many polynomials used in high school math will follow that form, or one that is similar. If it is an expression, the variable x can take a number of different values. If they are in an equation or an inequality, the solution set for the variable will either consist of many solutions, one solution, or no solutions.
Figure 1: Check the form the polynomial takes before finding factors or a numerical solution.
Review for Common Factors
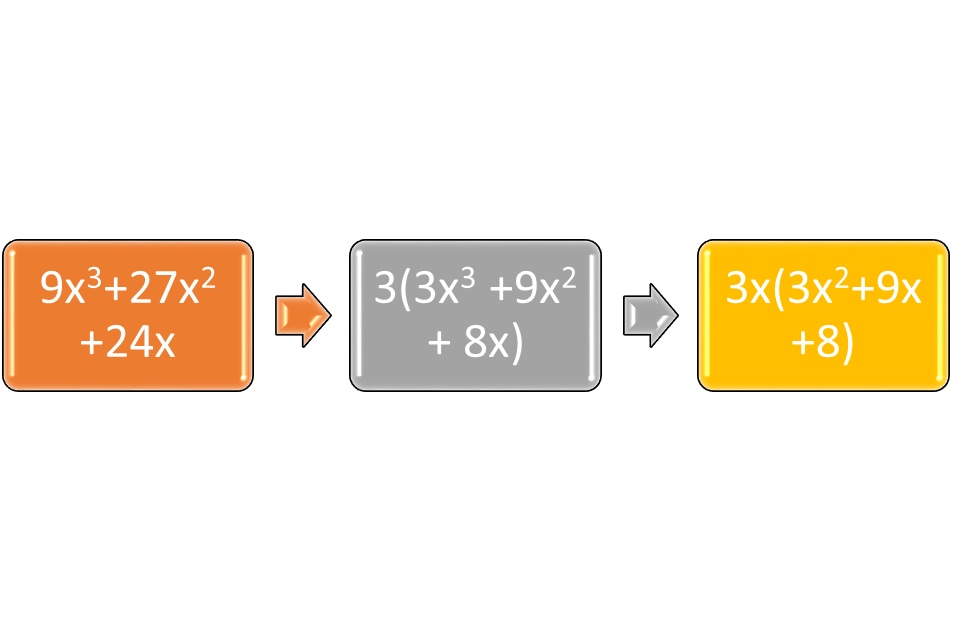
If the polynomial expression has common factors other than 1 or -1, the common factors can be factored out, before looking at the rest of the equation. This is a very important step, because the polynomial that is left may be an ax2 +bx +c expression. Suppose the expression is 9x3 + 27x2 + 24x. The common factor to each element of the expression is 3x. Dividing 9x3 by 3xis 3x2; 27x2 by 3x is 9x, and 24x by 3x is 8. Therefore one factor is 3x, and the other factor is in the form ax2 +bx +c.
Figure 2: An example of reviewing the polynomial for common factors.
Defining AC and Splitting the Middle Term
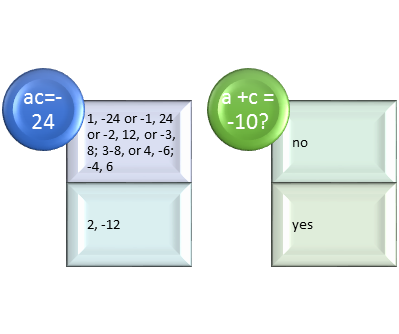
The next step is to multiply the leading coefficient a by the constant c. In this example 3∙8 is 24. In the polynomial 14x2 + 67x + 81, 14∙81 is 1134. In the polynomial x2 -3x + 7, 1∙7 is 7. In symbol terms, find integers p and q such that pq =ac. In symbol terms, integers p and q are such that pq =ac AND p + q =the coefficient b. Then the expression can be factored as (x +p) (x +q). This is also called splitting the middle term, and it is a method of trial and error. Suppose the expression is 3x2 -10x -8. The expression is in the form ax2 +bx +c. That a coefficient is 3, b is -10, and c is 8, so there are no common factors. In this example ac is equal to -24, so the task is to find two integers p and q, so that pq = -24 and p + q = -10. The factors that are equal to -24 are (-1, 24) with a sum of 23; (1, -24) with a sum of -23, (-2, 12) with a sum of 10, and (2,-12) with a sum of -10; (-3, 8) with a sum of 5; and (3, -8) with a sum of -5; (-4, 6) with a sum of 2, and (4, -6) with a sum of -2. The integers that follow both conditions are 2 and -12.
Figure 3: The process of defining AC and splitting the middle term.
Factoring by Grouping
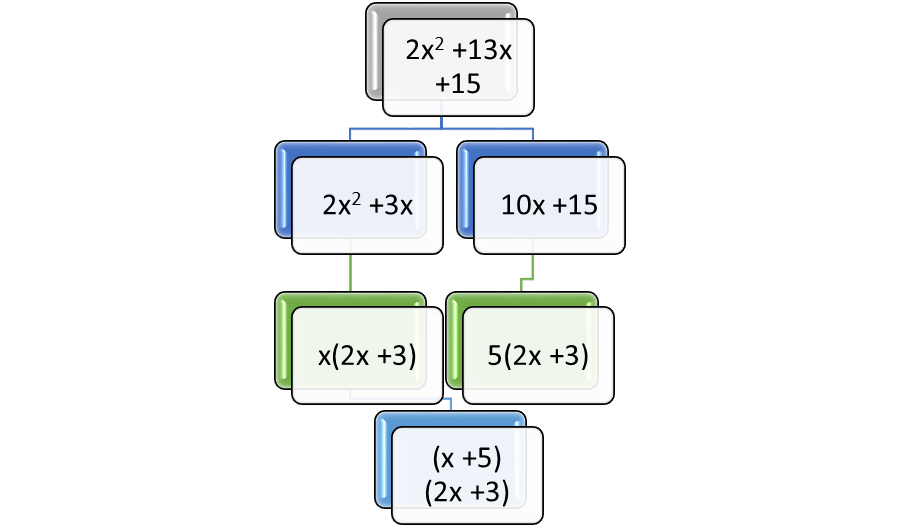
Next, write the expression out and group the factors. The polynomial 3x2 -10x – 8 = 3x2 – 12x + 2x – 8 = 3x(x – 4), because 3x ∙ x is 3x2 and 3x ∙ (-4) is -12x. Also 2x – 8 can be factored as 2(x – 4), because the expression 2x – 8 is equal to 2(x – 4). Putting the expression together 3x(x – 4) +2(x – 4) equals (3x + 2) (x – 4), which can be checked by multiplying using FOIL, so that 3x ∙ x = 3x2, 2x – 12x = -10x, and 2 ∙ 4 is 8.
Figure 4: An example of factoring by grouping.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Shiloh, PA: visit Tutoring in Shiloh, PA