Two triangles are said to be congruent if they have same shape and same size. When triangles are congruent corresponding sides (sides in same position) and corresponding angles (angles in same position) are congruent (equal).
There are two theorems and three postulates that are used to identify congruent triangles.
Angle-Angle-Side Theorem (AAS theorem)
As per this theorem the two triangles are congruent if two angles and a side not between these two angles of one triangle are congruent to two corresponding angles and the corresponding side not between the angles of the other triangle.
Example:
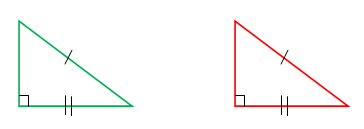
Hypotenuse-Leg Theorem (HL theorem)
If the hypotenuse and one of the legs (sides) of a right triangle are congruent to hypotenuse and corresponding leg of the other right triangle, the two triangles are said to be congruent.
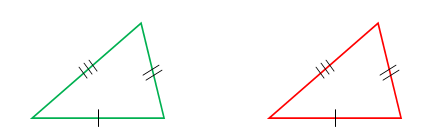
Side-Side-Side Postulate (SSS postulate)
If all three sides of a triangle are congruent to corresponding three sides of other triangle then the two triangles are congruent.
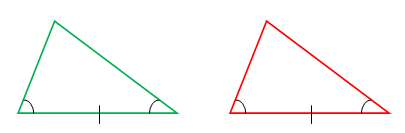
Angle-Side-Angle Postulate (ASA postulate)
According to this postulate the two triangles are said to be congruent if two angles and the side between these two angles of one triangle are congruent to corresponding angles and the included side (side between two angles) of the other triangle.
Side-Angle-Side Postulate (SAS postulate)
If two sides and the included angle (angle between these two sides) of one triangle are congruent to the corresponding two sides and the included angle of a second triangle, then the two triangles are congruent.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Vancouver visit: Tutoring in Vancouver.