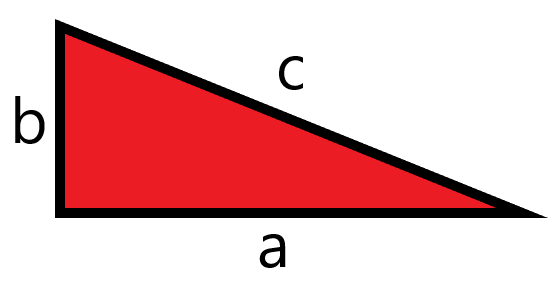
The Pythagorean Theorem relates the lengths of the three sides of any right angle triangle. The two sides of the triangle that meet at the right angle are normally labelled as having lengths “a” and “b”, and the hypotenuse, which is the long side of the triangle, opposite the right angle, is labelled with the variable “c”.
The Pythagorean Theorem relates the side lengths according to the following equation:
a² + b² = c²
This theorem allows you to find the length of the third side of a triangle if you know the first two side lengths and you know you are dealing with a right angle triangle.
This theorem also allows you to determine if a triangle is a right angle triangle when you are given the lengths of all three sides.
Here are some examples:
Example One: Find the length of the remaining side in the given right angle triangle.
____________________80
48
The first step is to identify what information we are given.
From the diagram we know that c = 80 and a = 48 (it does not matter if we call this side a or b, the important part is that c is referring to the hypotenuse).
a² + b² = c²
48² + b² = 80²
2304 + b² = 6400
b² = 4096
b = 64
Therefore, we have found that the length of the missing side to 64.
Example Two: Given the three side lengths, determine if the triangle is a right angle triangle.
45 55
___________75
We need to see if the squares of the two sides which meet at the right angle equal the square of the length of the hypotenuse.
By looking at the triangle we can see that the angle most likely to be equal to 90 degrees in the angle appearing at the top of the triangle.
The squares of the two sides which meet at the right angle is:
45² + 55² = 2025 + 3025 = 5050
The square of the length of the hypotenuse is:
75² = 5625
Therefore, we can conclude that this triangle is not a right angle triangle.
Looking to do the PSAT? We can help with PSAT Prep
This article was written for you by Mia, one of the tutors with Test Prep Academy.