Overview of the Quadratic Formula
The Quadratic Formula is a special math expression that can be used to help students solve math equations that take a distinct form:
ax2 + bx + c = 0
Quick Factoring to Solve the Problem
There are 2 things to remember. First, a, b, and c are numbers (the coefficients) and they are always given in the problem, so they are always known. It’s the x that’s the unknown. Second, although the Quadratic Formula works, sometimes it’s easier to factor the problem and solve fox x that way.
For example, suppose you are already given a problem such as (x-2)(x-5) =0. That is already another representation of the Quadratic Equation and can be expanded into ax2-7x +10 = 0. (Using our definition of coefficients, a equals 1, b = -7, and c =10).
Rather than use the formula, it’s easier to just think that if the answer is zero, either x-2 = 0, in which case x has to equal 2 or x -5 has to equal 0. Then X equals 5.
Solve for X using the Quadratic Formula
Not every equation can be easily factored, though. Therefore, the other part of the Quadratic Formula becomes important. If we already know a, b, and c, x can be represented by a rather complicated formula that is simpler than it looks: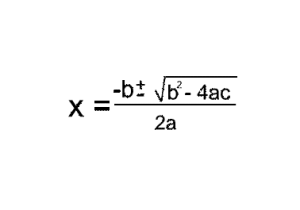
Remember to take each step in order and that way you will be able to solve for x, even if the equation can’t be factored easily (or if it isn’t already factored).
Always Check Your Work
Does it work in the real world? The previous equation was x2 -7x +10 =0. The numerator can be solved as 7 ± 3 {49-4(1)(10)} which is either 7 +3 or 7-3. 10/2 =5, and 4/2 = 2. Those were the answers for x that were solved by factoring the equation.
