The Pythagorean Theorem
The Pythagorean Theorem is one of the most useful tools in geometry, allowing us to determine the length of a given side of a right triangle as long as we know the lengths of the other two sides. It is important to remember that this only works for right triangles (triangles where one interior angle is 90 degrees).
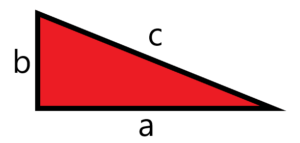
If we label the side lengths of a right triangle as 
, 
, and 
as in the diagram above, with being the hypotenuse (the length of the longest side), the Pythagorean Theorem states that:
![\[a^2 + b^2 = c^2\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-8283c19f4872ec3ad8dab6d31eb33b05_l3.png "Rendered by QuickLaTeX.com")
Proving the Pythagorean Theorem
Before we can see how the Pythagorean Theorem is useful, we must make sure that it is correct. Let us consider the diagram below, where we have a square constructed by joining 4 right triangles with side lengths of , , and .
The area of this square could be calculated by multiplying its width by its height. This would give:
![\[A=(a+b)(a+b)\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-73e61ddf2f8d31cc3fda177195ace804_l3.png "Rendered by QuickLaTeX.com")
We could also calculate the area by adding the areas of the four green triangles to the area of the smaller white square. The area of one green triangle is 
and the area of the white square is 
, so we get our second equation for the area of the large square:
![\[A=c^2+2ab\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-92ba8f9b0817f6a2c0d07ebe21cbd961_l3.png "Rendered by QuickLaTeX.com")
We can then equate these two equations for the area as they are both helping us find the area of the same square. This gives the following:
![\[(a+b)(a+b)=c^2=2ab\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-30a8f284292a76de52d3b5aa45e5b4af_l3.png "Rendered by QuickLaTeX.com")
If we expand the left side of this equation, we get:
![\[a^2+2ab+b^2=c^2+2ab\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-5d89c7554ef609ff467a42743c4a1cd8_l3.png "Rendered by QuickLaTeX.com")
Each side of the equation has the term 
, so if we subtract this term from both sides we are left with the Pythagorean Theorem:
![\[a^2+b^2=c^2\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-71ac3ac58938cc30b0ee3dd4646a2835_l3.png "Rendered by QuickLaTeX.com")
Examples
Now that we have proven the Pythagorean Theorem, it is instructive to see it in action. Broadly speaking, there are two types of problems that the Pythagorean Theorem helps us solve:
- We know the lengths of two sides of a triangle where neither is the hypotenuse.
- We know the length of the hypotenuse and one other side.
We will look at an example for each case.
Finding the Length of the Hypotenuse
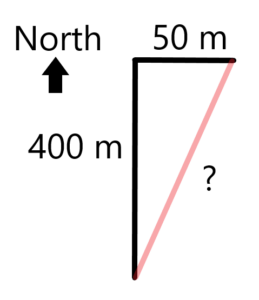
Let’s say that you are walking through your neighborhood and you travel 400 m North. You then turn and travel 50 m East. You might wonder how far away you are from where you started. Even though you walked a total of 450 m, it was not all in the same direction, so you aren’t sure exactly how far away you are from where you began. How would we solve this?
We could construct a diagram as shown above to help solve this problem. The path we travelled forms two sides of a right triangle, with the third side (the hypotenuse) forming the last side of our triangle. Let’s use the Pythagorean Theorem to figure out how far we are from our origin. If is 400, and is 50, then we insert those values into the Pythagorean Theorem as shown below:
![\[400^2+50^2=c^2\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-dfbd7451391b8d8355c1820956c6801d_l3.png "Rendered by QuickLaTeX.com")
Here we have used instead of a question mark. We can simplify this equation to be:
![\[162,500=c^2\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-da8ef2387308d0a76d94e35d535ef4dd_l3.png "Rendered by QuickLaTeX.com")
We then take the square root of both sides to find :
![\[\sqrt{162,500}=403.11=c\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-42a68cb4db0ac94713a2bcd0cfdb3f49_l3.png "Rendered by QuickLaTeX.com")
We find that in our 450 m of walking, we have only ended up a little over 403 m from where we started!
Using the Hypotenuse and One Other Side
As another example, supposed that we are trying to find the dimensions of a certain rectangle. As shown below, its length is 4 and we know that the length from corner to corner is 5. What is the rectangle’s width?
We can see that the length, width, and blue line connecting the corners forms a triangle. We could insert the known values into the Pythagorean Theorem to get:
![\[4^2+b^2=5^\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-420e6284d3b768c36379f5ade2972eb2_l3.png "Rendered by QuickLaTeX.com")
Here we have let be the width of our rectangle. We can simplify our equation to get:
![\[16+b^2=25\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-bdebf42ad18febafd9ca23d767bacaed_l3.png "Rendered by QuickLaTeX.com")
We then subtract 16 from both sides to get:
![\[b^2=9\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-49fde902c39eaddbd67e411d3102893a_l3.png "Rendered by QuickLaTeX.com")
Finally, we take the square root of both sides to get:
![\[b=\sqrt{9}=3\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-4e804bf30edc66ed488d177d23cd3dec_l3.png "Rendered by QuickLaTeX.com")
We find that the width of our rectangle is 3!
This has been a brief introduction into the Pythagorean Theorem along with some examples of its usefulness. For more information on this topic as well as assistance with homework and test preparation, feel free to reach out to an Academic Director toll-free at 1 (877) 545-7737 or via our Contact Us page.
Powered by WordPress with QuickLaTeX
