What is Factoring?
One of the most intuitive ways to approach factoring is to think of it as the opposite of expanding. This is demonstrated below (working from left to right):
Expanding:
![]()
Factoring:
![]()
This means that if we know how to expand, we can always check if our answer to a factoring problem is correct by making sure that when we expand we get the expression that we started with. This is similar to using subtraction to check addition, or multiplication to check division.
How to Factor
Here we will be showing how to factor polynomials where each term shares a common factor. Other methods of factoring do exist, but will be covered in a later post. This method of factoring has four steps:
- Determine the greatest common factor (GCF) of the terms in the algebraic expression.
- Divide each term by the GCF.
- Enclose the result of step 2 in brackets.
- Place the GCF outside of the brackets from step 3.
Let’s look at an example!
Suppose that we want to factor the following expression:
![]()
Let’s follow the steps we just outlined.
- We have two terms:
 and
and  . To find the GCF of these terms, we first find the largest common factor of
. To find the GCF of these terms, we first find the largest common factor of 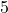 and
and 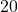 . This is
. This is 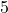 . We then want the GCF of
. We then want the GCF of  and
and  . This is
. This is  . We then combine this information to conclude that the GCF of our terms is
. We then combine this information to conclude that the GCF of our terms is 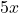 .
. - We now divide each term by
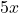 .
.  and
and 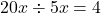
- We now place the result of step 2 in brackets to get:
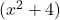
- Finally, multiply our result from step 3 by the GCF to get:

We have now successfully factored our expression. We can then multiply each of the terms by ![]() to confirm that we did the factoring correctly.
to confirm that we did the factoring correctly.
Why do We Factor?
Now that we have seen how to factor, you might wonder why this is important. An example is instructive. Consider the following expression:
![]()
This might initially look like a complicated expression, but it is important to notice that we can factor the numerator. The GCF of the terms in the numerator is ![]() . If we use that to factor the numerator our expression now looks like this:
. If we use that to factor the numerator our expression now looks like this:
![]()
Since we are multiplying and dividing by ![]() (opposite operations) we can “cancel out” the
(opposite operations) we can “cancel out” the ![]() in both the numerator and denominator to get the simplified expression:
in both the numerator and denominator to get the simplified expression:
![]()
Note: This is true as long as ![]() . See our post on asymptotes and holes if you’re interested in what happens if
. See our post on asymptotes and holes if you’re interested in what happens if ![]() .
.
This shows us that factoring can be a powerful tool to manipulate and simplify algebraic expressions, potentially allowing us to solve problems that would otherwise be complicated.
This has been a brief introduction to the concepts of factoring. For more information on this topic as well as assistance with homework and test preparation, feel free to reach out to an Academic Director toll-free at 1 (877) 545-7737 or via our Contact Us page.
Powered by WordPress with QuickLaTeX


