Overview
The tangent of an angle is a ratio of the length of a leg opposite an acute angle to the length of a leg adjacent to the acute angle in a right triangle. It is one of the basic trigonometric functions, and is related to many real-world measures of angles and navigation.
Definition
A right triangle has a number of special relationships between the measurements of its sides and angles. The Pythagorean Theorem (a2 + b2 = c2) relates the measurements of the sides of a right triangle. In any right triangle, there is one right angle, and two acute angles. The legs are the sides on either side of the right angle, and the hypotenuse is the long side of the triangle. If one leg is measured as a, and the other leg is measured as b, then the hypotenuse is measured as c. The tangent is the ratio of the measurement of the two legs of the angle, the one opposite the angle, and the one adjacent to the angle.
Figure 1: The definition of a tangent.
Applications
In the real world, there are many things that are similar to right triangles that need measurement. Trees grow perpendicular to the ground, the mast of a sailboat is perpendicular to the water, and a line can be drawn from the top of a mountain to a base camp at sea level. A lighthouse stands on a cliff perpendicular to the sea.
Examples
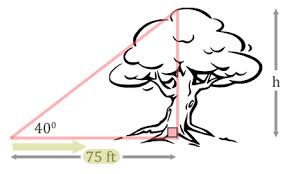
Suppose a person has to look up at a 400 angle to see the top of a tree that is 75 ft. away. The height of the tree can be found by using a tangent, which can be measured as 0.8390, the ratio of both legs of the triangle formed by the distance the person is from the tree (75 ft.), and the perpendicular line to the top of the tree. (The hypotenuse of the right triangle is the line of sight.) The other leg of the triangle can be measured as 75(.8390) = 62.93 feet, or about 63 feet tall, which is within the average height range for many trees, including maple, spruce, and aspen.
Figure 2: Using a tangent to estimate the height of a tree.
The Slope of a Line
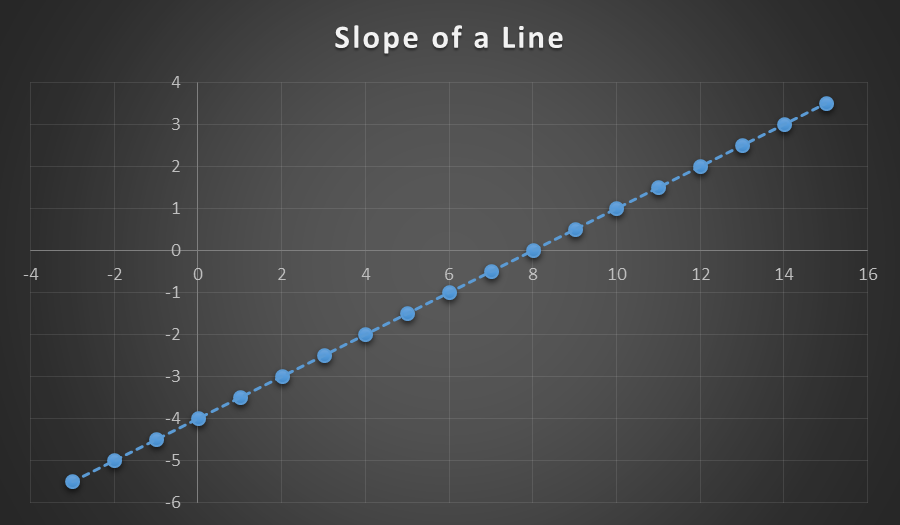
The slope of a line can also be measured by a tangent. Suppose a line such as y = 1/2x -4 is graphed. It crosses the y axis at (8, 0) and the x axis at (0, -4). The slope of the line is ½, which is the same as the tangent of the angle formed by the line as it crosses the x axis.
Figure 3: The tangent is the same as the slope of a line.
Interested in trigonometry tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Lexington, VA: visit Tutoring in Lexington, VA