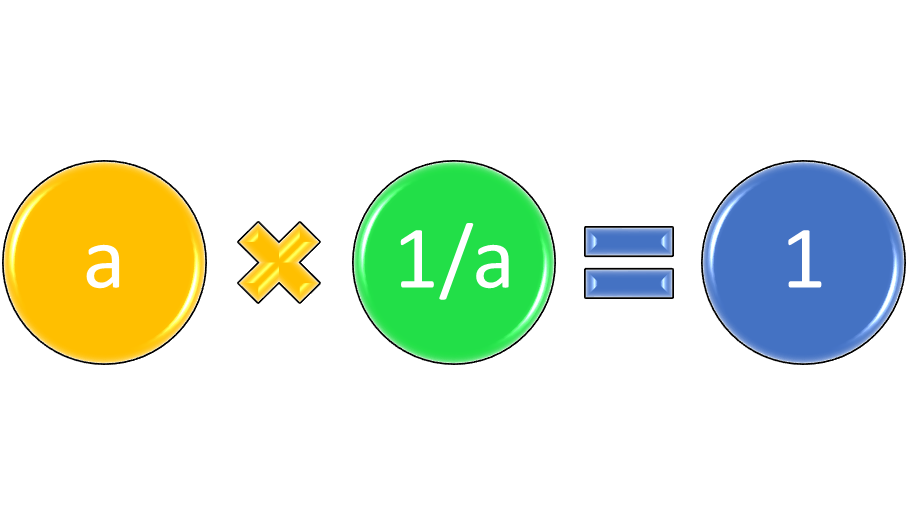Overview
Both sides of an equation will remain equivalent as long as we add, subtract, multiply and divide by equivalent expressions. The properties of equality ensure that we can isolate and solve for variables.
Equivalent Equations
When two or more equations have the same solution, they are equivalent equations. For example, equations such as 2x – 4 = 0, 2x = 4, and x = 2 all have the same solution. When equivalent equations are substituted for one another, the form of the equation may change, but the meaning of the equation remains the same. It may just be in a form that is more easily solved.
Addition Property of Equality
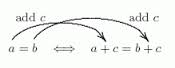
The Addition Property of Equality in symbol form states that if a = b, then a + x = b + x. In other words, the same number can be added to both sides and the equations will still be equivalent. Therefore, 2x – 4 + 4 = 0 + 4, as the same number, 4, has been added to both sides. The equivalent equations are 2x = 4, as -4 + 4 equals 0 and can be eliminated from the first equation. The Addition Property of Equality also holds for subtraction, as the definition of subtraction is adding the inverse. Thus a – b is equivalent to a + (-b). The Addition Property of Equality can be used to isolate a variable on one side of the equation so that it can be solved. Suppose that y + 3 = 10. Then y + 3 -3 + 10 – 3, or y = 10 – 3, or y = 7. It is very important to solve for the variable by adding the same number to both sides of the equation, and to choose a number that will isolate the variable on one side of the equation. In the example, y + 3 = 10, the -3 isolated the variable y on the left side of the equation, and it was subtracted from both sides to keep the equations balanced.
Figure 1: The Addition Property of Equality in symbol form.
Reciprocals
A reciprocal is the multiplicative inverse of any real number, so that the number times its reciprocal is equal to 1. In symbol form b ∙ 1/b =1 for any real number where b is not equal to 0. The number 0 has no reciprocal because division by 0 is undefined. For example, if b equals 100, 1/b equals 1/100, because 100 ∙ 1/100 is equal to 1. Similarly, if b equals 3/5, its reciprocal 1/b equals 5/3, because 3/5 times 5/3 is equal to 1.
Figure 2: A number multiplied by its reciprocal equals 1.
Multiplication Property of Equality
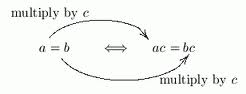
The Multiplication Property of Equality is similar to the Addition Property of Equality. In symbol form, if a =b, then ax = bx. The difference is that the Multiplication Property is used when the coefficient of the term is something other than 1. For example, if 2x = 4, the coefficient of x is 2. The Multiplication Property of Equality is also used to isolate a variable to one side of the equation so it can be solved. In order to isolate the x on the left side of the equation, both sides of the equation are multiplied by the reciprocal of 2, or ½ so that 2x ∙ 1/2 = 4 ∙ ½, or x = 2. In this example, both sides are multiplied by ½ to keep the equation balanced.
Figure 3: The Multiplication Property of Equality in symbol form.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Elsmere, DE: visit Tutoring in Elsmere, DE