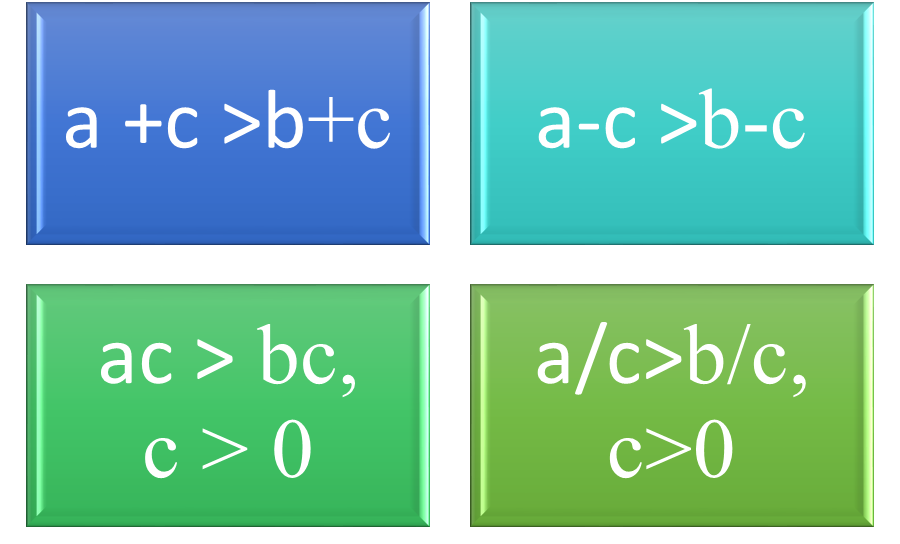Overview
Linear inequalities in one variable can be solved similarly to linear equations in one variable. Properties that hold for linear inequalities include properties of addition, subtraction, multiplication, and division, as well as those involving relationships between negative numbers.
Properties of Inequalities
There are four properties of inequalities that hold true for real numbers. The addition property of equality in symbol form is: if a > b then a + c > b + c. Similarly, for subtraction, if a > b, then a – c > b –c. For the properties of multiplication and division, c must be greater than 0. If a > b and c > 0, then ac > bc. Similarly, if a >b and c > 0, then a/c > b /c. Suppose that the inequality is x -5 >-2. The variable can be isolated on the left side of the equation to solve it, so that x > -2 + 5, or x > 3. Also, a > b means the same thing as b < a.
Figure 1: Properties of inequality in symbol form.
Multiplying by Negative Numbers
The properties of inequalities for multiplication and division specify that the real number c is greater than 0 for the relationship to hold. What happens if c is a negative number? Suppose the inequality is 5 > 3, and both sides were multiplied by -4. 5(-4) is -20 and 3(-4) is -12. The relationship is -20 < -12, so the direction of the sign changes. Similarly, suppose that 100 > 80, and both sides were divided by -10. 100/-10 is -10 and 80/-10 = -8. The relationship is -10 < -8, so the direction of the sign also changes for division.
Inequalities When the Variable Is on Both Sides of the Sign
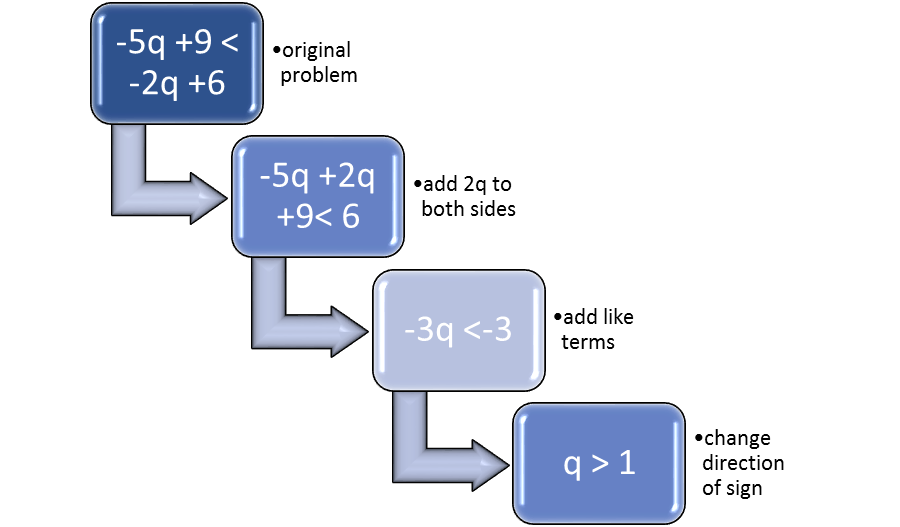
Inequalities with the variable on both sides of the sign are solved similarly to equations with the variable on both sides of the equals sign. Suppose the expression is -5q + 9 < -2q + 6. To solve the inequality, -5q + 2q + 9 < -2q + 2q + 6, or -3q + 9 < +6, or -3q < 6 – 9, or -3q < -3. Since dividing by -3 will change the sign, q > 1.
Figure 2: Process of solving inequalities when the variable is on both sides of the sign.
Linear Inequalities with All Solutions or No Solution
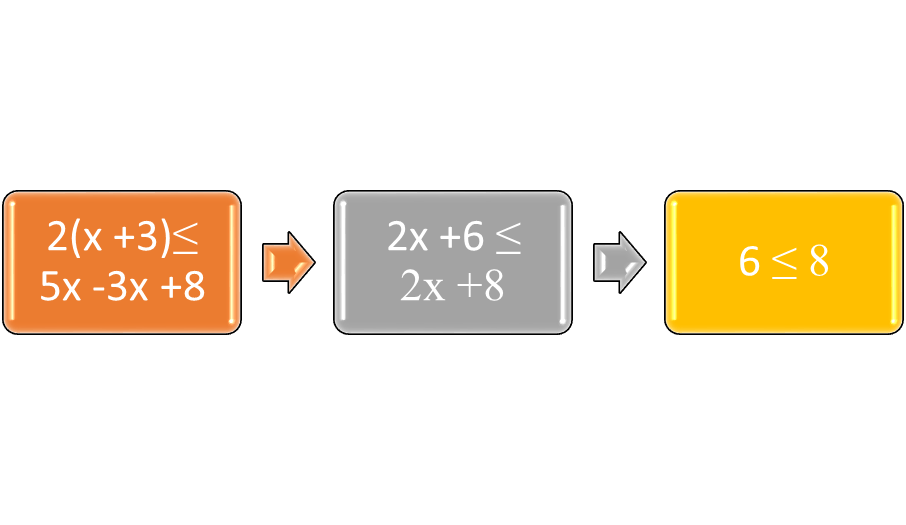
Similar to equations with all real numbers as the solution set, some inequalities have all real numbers as their solution set. Suppose the inequality is 2(x + 3) ≤ 5x -3x + 8. It can be simplified as 2x + 6 ≤ 2x + 8, or 6 ≤ 8. The statement is true for all real numbers.. Suppose the inequality is 3(x + 1) > 3x + 5. Then 3x + 3 > 3x + 5. There is no real number such that 3 > 5, so there is no solution.
Figure 3: An example of an inequality that is true for all real numbers.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Kahului, HI visit Tutoring in Kahului, HI