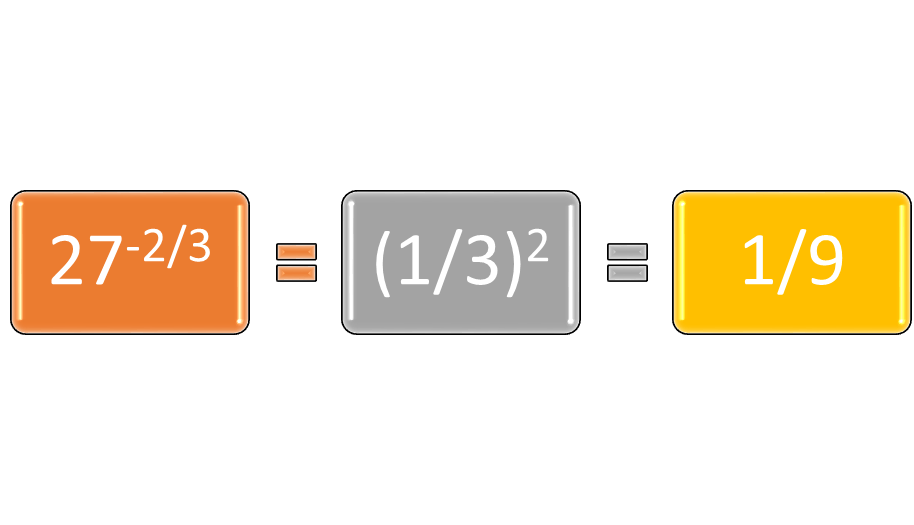Math Review of Higher Roots and Rational Exponents

Overview

Cube and fourth roots follow rules similar to those for square roots. The rules for rational exponents are an extension of the rules for exponents and roots.

Cube Roots

If any real number b³ equals c, then b is the cube root of c, when b is not equal to 0. For example, 2³ equals 8, so 2 is the cube root of 8. Similarly, 3³ equals 27, so 3 is the cube root of 27. The cube root of a positive number is a positive number, because a positive times a positive times a positive is a positive. A negative number, such as -125, can have a real cube root, such as -5, because -5³ is -125. Although a negative number times a negative number is a positive number, that positive number times a negative number is a negative number.

Figure 1: The definition of cube roots in symbol form.

Fourth Roots

If any real number b⁴ equals c, then b is the fourth root of c, when c is a positive number. For example, 4⁴ is equal to 256, so 4 is the fourth root of 256. Similarly, 10⁴ equals 10,000, so 10 is the fourth root of 10,000. The fourth root of a positive number is a positive number. The fourth root of a negative number is not a real number, similar to the square root of a negative number.

Positive Rational Exponents

A rational exponent such as x^1/2 is the same thing as the square root of x, √x. Similarly, a rational exponent such as x^1/3 is the same thing as the cube root of x, and x^1/4, as the fourth root of x. The definition can be extended to other rational exponents as well. For example, 8^2/3 means the same thing as the cube root of 8, which is 2, squared which is 4. Recall that the cube root of 8 is 2, and that 2¹ is equal to 2. Therefore, x^1/3 is the cube root of x¹, and x¹ equals x for all real numbers.

Figure 2: Rational exponents of real numbers.

Negative Rational Exponents

Recall that a negative exponent, a^-x, means the same thing as 1/(a^x), so that 3^-2 means the same thing as 1/3², or 1/9, and so on. That definition holds true for negative rational exponents, so that 27^-2/3, means the same thing as 1 over the cube root of 27, which is 3, squared. Then, (1/3)² is 1/9.

Figure 3: Solving a negative rational exponent.

Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.

SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Nampa, ID: visit Tutoring in Nampa, ID