Overview
Real numbers include rational and irrational numbers, whole numbers, positive and negative integers, and the number 0. They can be used in operations such as addition, subtraction, multiplication, and division, as well as in expressions involving variables.
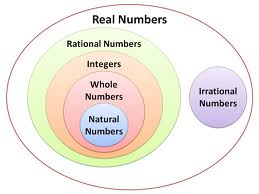
Real Numbers
Real numbers include many different types of numbers that are familiar, such as positive and negative integers, along the number line. Rational numbers, such as 3/5, are also included, as well as irrational numbers such as π, √7, and √2. The representation of infinity ∞ is not a real number, nor are imaginary numbers.
Figure 1: Contents of the set of real numbers.
Addition of Real Numbers
Since real numbers fall on the number line, they can be added using the number line model. For example, to add 3 + 2, go from 0 to 3 on the number line, and then forward 2 spaces to 5. Similarly, adding -2 + -5, go left on the number line 2 spaces to -2 and then go left 5 more, to -7. Fractions can be added by finding the least common denominator, then adding them using the number line, because fractions are rational numbers.
Figure 2: Addition of real numbers using the number line model.
Subtraction of Real Numbers
Subtraction is the same thing as adding the additive inverse of the number to be subtracted. In symbol form, for any two numbers a and b, a – b is the same thing as a + (-b). Recall that the additive inverse of a number is the opposite of that number, so that a + (-a) = 0, and b + (-b) = 0. Subtraction can also be demonstrated using the real number line model, so that subtracting 7-6 is a matter of starting at 0 and going 7 spaces to 7, then going to the left 6 spaces, to 1.
Figure 3: Definition of subtraction in symbol form.
Multiplication and Division of Real Numbers
There are two important rules to remember when multiplying numbers. The product of two positive numbers or two negative numbers is a positive number. The product of a positive number and a negative number is a negative number. For example, 6∙ 2 is 12, as the product of two positive numbers. Similarly -5 ∙ -6 is 30, as the product of two negative numbers. However, -7 ∙ 3 is -21, as the product of a negative number and a positive number, and 4 ∙ -7 is -28, as the product of a positive number and a negative number. The rules for dividing numbers are similar. If both numbers are positive, the quotient will be positive, or if both numbers are negative, the quotient is positive.
Figure 4: Rules for multiplication and division of real numbers.
Interested in pre-algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Kokomo, IN: visit Tutoring in Kokomo, IN