Overview
A complex rational expression contains a fraction within a fraction. In math language, it is a rational expression that has one or more rational expressions contained within the numerator, denominator, or both. It may or may not contain variables within it. The fractions in the numerator or denominator must be simplified first, before the other rational expression can be tackled.
Definitions
A rational expression is a ratio. Examples of simple ratios that do not contain variables are 2/3, 6/7, and 7/8. Rational expressions can also include variables, such as (3x)/7, (9z + 2)/4, or 3/(y + 1). They can be simplified in one or two steps. Complex rational expressions (also called complex fractional expressions) are ratios that contain fractions within fractions. Simplifying them often takes more than one or two steps.
Figure 1: A complex fraction in symbol form.
Simplifying the Numerator
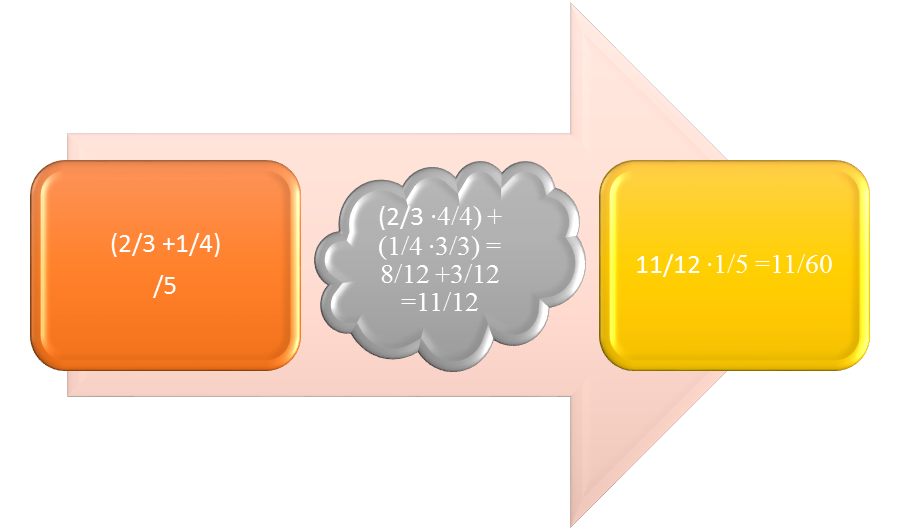
Suppose a rational expression contains the terms (2/3 + 1/4) in the numerator and 5 in the denominator. In one method, the first step in simplifying the rational expression is to find the LCM for the fractions in the numerator, changing each fraction to the equivalent common denominator, and performing the operation. In this example 2/3 becomes 8/12 and ¼ becomes 3/12. Adding 8/12 and 3/12 equals 11/12. If one or more variables in the rational expression is in the numerator, the process is similar. Suppose another complex rational expression contains a variable in the numerator, so that the terms are ([4x]/7 + x/9)/2. In that case, the first step would be similar: The LCM of 7 and 9 is 63, so the numerator becomes 36x/63 + 7x/63 or 43x/63. The denominator is still 2.
Figure 2: Simplifying the ratio when a fraction is in the numerator.
Simplifying the Denominator
If the rational expression is in the denominator, the process is similar to solving the rational expression in the denominator. However, if there is a variable in the denominator, the denominator cannot equal zero. That would be the same thing as dividing by zero, which is undefined by definition. Suppose the numerator is 3 and the denominator is 11/12 + 1/20. Using the same method, the LCM is 60, so the fractions in the denominator become 55/60 + 3/60 or 58/60. (In turn, 58/60 can be simplified to 29/30.) The rational expression becomes 3/(29/30).
Figure 3: Simplifying the ratio when a fraction is in the denominator.
Simplifying the Entire Ratio
Whether the expression is (11/12)/5, (43x/63)/2, 3/(29/30), 12/(3x + 1)/2, or even (3/(2x + 1)/1/2), solving the ratio in the numerator or denominator is only part of the process. The ratio is not fully simplified until the fraction within the fraction is done. Suppose the expression is (11/12)/5. That is equal to 11/12 ∙ 1/5 = 11/60. Similarly, (43x/63)2 means the same thing as 43x/63 ∙ ½ or 43x/126.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Guthrie, OK: visit Tutoring in Guthrie, OK