Conservation of Energy
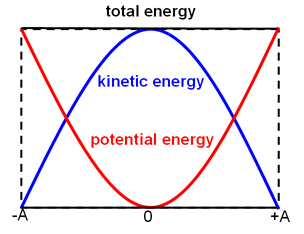
The idea of conservation of energy is that energy cannot be created or destroyed, it can only be changed into a different form. Different forms of energy include sound, heat, light, kinetic and potential. If a ball is dropped from the sky from rest, it begins with a large amount of gravitational potential energy, and as the ball falls, the amount of gravitational potential energy decreases. But where does it go?
As the potential energy decreases, the ball’s kinetic energy is increasing as the ball accelerates towards the group. In the real world, some energy will be transformed into heat due to air resistance and friction, and sound energy when the ball hits the ground.
We can use the idea of conservation of energy to determine some unknown quantities as demonstrated in the following example.
If a 2.00 kg ball is thrown downwards at a speed of 5.00 m/s off a 10.0 m high building. What will the ball’s speed be when it hits the ground ignoring friction and air resistance?
We know by the conservation of energy that the amount of energy in this problem must remain consistent. Therefore the gravitational potential energy must be converted into kinetic energy when the ball hits the ground. We can then set up this equation.
(Energy at start) = (Energy at end)
KE1 + PE1 = KE2
½ mv12 + mgh = ½ mv22
½ (2)(5)2 + (2)(9.8)(10) = ½ (2)v22
25 + 196 = v22
221 = v22
14.9 m/s = v2
Thus the ball’s speed will be approximately 14.9 m/s when it hits the ground.
We can see that the mass of the ball does not matter in regards to the problem as it simply cancels out. Conservation of energy is a useful tool for solving problems with a few unknowns.
Looking to get ready for the ACT? We can help with ACT Prep
This article was written for you by Jeremie, one of the tutors with Test PrepAcademy.