Overview
When the coefficient of the squared term is greater than 1, an extra step is added to factoring the trinomial. It can be factored by either using FOIL or a modified form of factoring by grouping.
Factoring the Squared Term
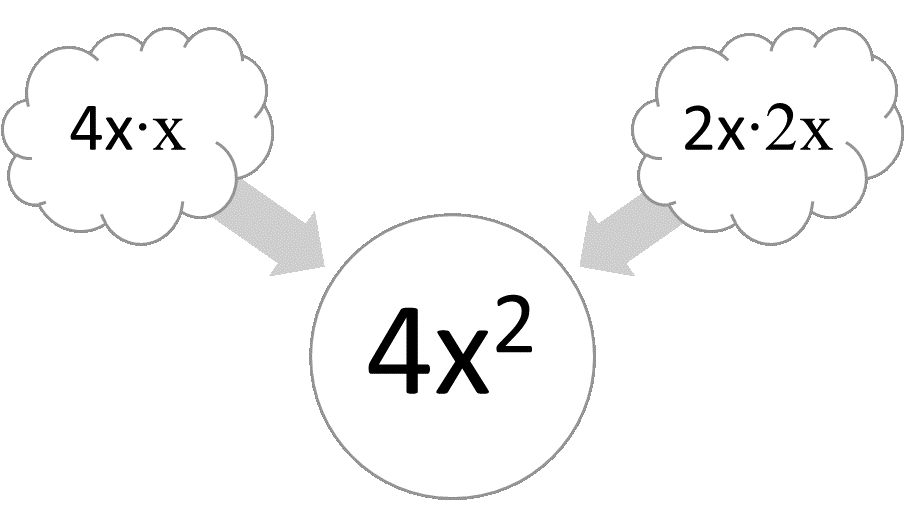
When the squared term of a quadratic trinomial is x2 with a coefficient of 1, it always factors as (x + y)(x + z). If the coefficient is greater than 1, the factors of the squared term must be considered. Suppose the squared term is 2x2. Its factors are 2x and x. If the squared term were 4x2, it would have even more possibilities: x and 4x, 2x and 2x.
Figure 1: Factoring the squared term when the coefficient is greater than 1.
Choosing Factors Using FOIL
Factoring is the reverse of multiplying. The expression (2x + 3)(x + 5) is equal to 2x2 + 13x + 15. The product of the first terms is equal to 2x2. The middle term is derived from the sum of the products of the outer terms, 10x, and the inner terms, 3x. The product of the last terms is equal to 15. Using this logic, the factoring for 2x2 + 7x + 6 can be derived similarly. The squared term can be factored as 2x times x. The constant has more possibilities, 1 and 6, 6 and 1, 2 and 3, or 3 and 2. For example, (2x + 1) and (x + 6) can be paired, or (2x + 6) and (x +1). Similarly, (2x + 3) and (x + 2) can be paired, or (2x + 2) and (x + 3). Suppose (2x + 1) and (x + 6) are paired. In that case, x + 12x equals 13x, which is too high. If (2x + 6) and (x + 1) are paired, then 2x +6x equal 8x, which is also too high. Suppose (2x + 2) and (x + 3) are paired. Then 6x and 2x equal 8x, which is also too high. That leaves (2x +3) and (x + 2). In that case 4x and 3x equal 7x, which is the correct alternative.
Figure 2: Choosing factors using FOIL.
Choosing Factors by Grouping
When factoring by grouping, rewrite the trinomial with 4 terms rather than 3, as 2x2 + 3x + 10x + 15). The first group can be factored as x (2x + 3) and the second group as 5(2x + 3). Using the distributive property, the factors are (x + 5)(2x + 3), which is equivalent to (2x + 3)(x + 5). Similarly, the trinomial 2x2 + 7x + 6 can be rewritten as 2x2 + 3x + 4x + 6. The first group can be rewritten as x (2x + 3) and the second group can be rewritten as 2(2x + 3). Using the distributive property, the factors are (x + 2)(2x + 3).
Figure 3: Choosing factors by grouping.
Prime Polynomials
Suppose the polynomial is 2x2 + 3x + 7. It is in the form of ax2 + bx + c, where a equals 2, b 3, and c 7. In order to choose factors by grouping, a∙ c should equal b. In this case a is 2 and c is 7, and some of the factors of 14 are 1 and 14 and 7 and 2. The sum of 1 and 14 is 15 and the sum of 7 and 2 are 9, neither of which is equal to 3. That polynomial is a prime polynomial.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Cumberland, MD: visit Tutoring in Cumberland, MD