Rational Functions
Rational functions are functions of the form:
![]()
where ![]() and
and ![]() are polynomials. An important feature of many rational functions is the existence of asymptotes and/or holes.
are polynomials. An important feature of many rational functions is the existence of asymptotes and/or holes.
Asymptotes
An asymptote is a straight line that a rational function approaches, but never actually touches. There are three types of asymptotes:
- Vertical asymptotes
- Horizontal asymptotes
- Oblique asymptotes
Vertical Asymptotes
Vertical asymptotes occur at ![]() values where
values where ![]() (the denominator in a rational function) is zero but
(the denominator in a rational function) is zero but ![]() (the numerator in a rational function) is non-zero. We can see this in the following example:
(the numerator in a rational function) is non-zero. We can see this in the following example:
![]()
Here ![]() and
and ![]() . We see that at
. We see that at ![]() ,
, ![]() and
and ![]() . Thus, we have a vertical asymptote at
. Thus, we have a vertical asymptote at ![]() .
.
Horizontal Asymptotes
Horizontal asymptotes occur when a rational function approaches a specific ![]() value as
value as ![]() becomes very big in the positive or negative directions. If we return to our example function:
becomes very big in the positive or negative directions. If we return to our example function:
![]()
we can see that if ![]() is a very big negative number, then
is a very big negative number, then ![]() will get extremely close to 0. The same is true if
will get extremely close to 0. The same is true if ![]() is a very big positive number. This means that
is a very big positive number. This means that ![]() has a vertical asymptote at
has a vertical asymptote at ![]() . Thus, we have seen that
. Thus, we have seen that ![]() is an interesting function in that it has both a horizontal asymptote and a vertical asymptote. These are graphed along with
is an interesting function in that it has both a horizontal asymptote and a vertical asymptote. These are graphed along with ![]() below.
below.

Note the vertical (green) and horizontal (blue) asymptotes. f(x) gets infinitely close to these asymptotes without ever touching them.
Oblique Asymptotes
Oblique asymptotes occur when the degree of ![]() is one greater than the degree of
is one greater than the degree of ![]() .
. ![]() must also not be a factor of
must also not be a factor of ![]() . The degree of a polynomial is the highest power of
. The degree of a polynomial is the highest power of ![]() it contains. An oblique asymptote is a line that a rational function approaches for large values of
it contains. An oblique asymptote is a line that a rational function approaches for large values of ![]() . It is different from a vertical or horizontal asymptote in that it is not vertical or horizontal (it will have non-zero, definite slope). A good example of this is the function below:
. It is different from a vertical or horizontal asymptote in that it is not vertical or horizontal (it will have non-zero, definite slope). A good example of this is the function below:
![]()
Here, the degree of ![]() is two and the degree of
is two and the degree of ![]() is one. To find the equation of the line representing the oblique asymptote of
is one. To find the equation of the line representing the oblique asymptote of ![]() , we must divide the coefficient of the highest power of
, we must divide the coefficient of the highest power of ![]() in
in ![]() by the coefficient of the highest power of
by the coefficient of the highest power of ![]() in
in ![]() . In both cases, this coefficient is 1, so the equation of the oblique asymptote of
. In both cases, this coefficient is 1, so the equation of the oblique asymptote of ![]() is
is ![]() . This is visualized in the graph below:
. This is visualized in the graph below:
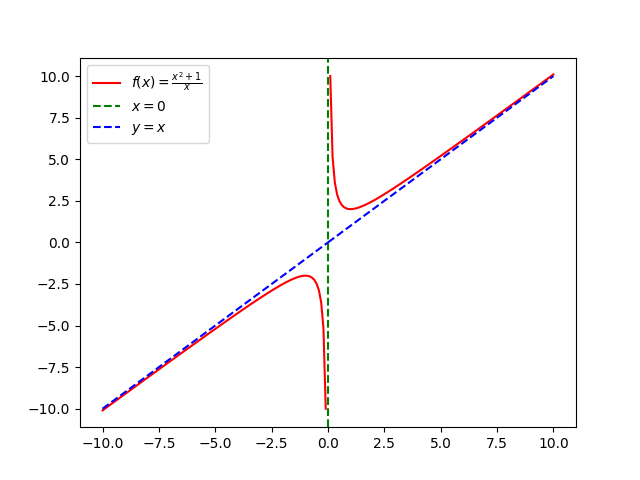
Note the oblique asymptote (blue) which operates similarly to a vertical or horizontal asymptote, except that it is “tilted” due to having non-zero, definite slope.
Holes
Finally, we want to consider holes. A hole occurs at any ![]() value where
value where ![]() and
and ![]() are both 0. Holes are aptly named, as they represent points where the function does not exist. They look like a hole in the graph of the function! A good example of this is the following function:
are both 0. Holes are aptly named, as they represent points where the function does not exist. They look like a hole in the graph of the function! A good example of this is the following function:
![]()
We can see that ![]() , so we have identified a hole at
, so we have identified a hole at ![]() . For all other
. For all other ![]() ,
, ![]() can be simplified to
can be simplified to ![]() . Thus, the graph of
. Thus, the graph of ![]() will be identical to the line
will be identical to the line ![]() except that the function does not exist at
except that the function does not exist at ![]() . This is shown in the graph below, with the whole represented as an unfilled circle.
. This is shown in the graph below, with the whole represented as an unfilled circle.
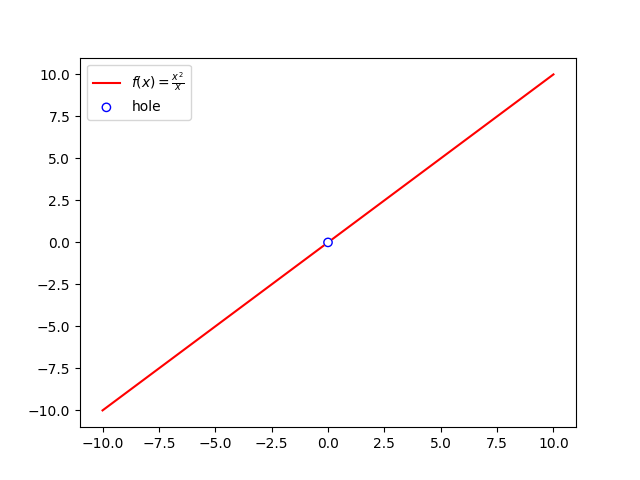
Note the hole at x=0. Aside from the hole, f(x) is identical to the line y=x. It is also important to remember that there is no oblique asymptote, as although the degree of the numerator is 1 greater than the degree of the denominator, the denominator is a factor of the numerator.
This has been a brief introduction into the concepts of asymptotes and holes in rational functions. For more information on this topic as well as assistance with homework and test preparation, feel free to reach out to an Academic Director toll-free at 1 (877) 545-7737 or via our Contact Us page.
Powered by WordPress with QuickLaTeX