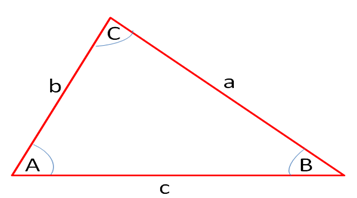
Law of cosines relates the lengths of sides of an oblique triangle (triangle that is not right-angled) to the cosine of one of its angles. This law is also known as cosine formula or cosine rule. The law of cosines can be used to find the third side of triangle when two sides and the enclosed angle is known, and to find the angles of triangles when all three sides are known.
If a, b, and c are the lengths of the sides of the triangle, and A, B and C are the opposite angles as shown below then according to cosine rule:
a2 = b2 + c2 – 2bccos(A)
b2 = c2 + a2 – 2cacos(B)
c2 = a2 + b2 – 2abcos(C)
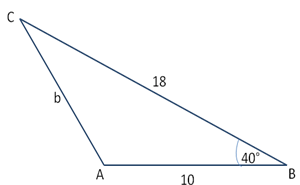
Example:
From the above figure we know, a = 18, c = 10 and angle B = 40°
As per Law of Cosines, b2 = c2 + a2 – 2cacos(B)
b2 = 102 + 182 – 2 × 10 × 18 × cos(40°)
b2 = 100 + 324 – 360 × 0.766
b2 = 148.24
b = sqrrt(148.24) = 12.17