Overview
Thinking about sets of objects and numbers is as simple as counting and as complex as infinity and transfinite numbers. Sets are an essential underlying concept of mathematics and logic.
Roster or Description
Mathematicians use the language of set theory to describe sets. For example, small, finite sets can be defined using the roster method, which is exactly like a team roster. Each player on the team roster can be listed as a member of a set, such as {Russell Wilson, Marshawn Lynch, Derrick Coleman, Percy Harvin, Luke Wilson …Jimmy Staten, Julius Warmsley}. The other term for sets is the description method, such as {players on the active list for the Seattle Seahawks}. Using math language, Set A = {3, 4, 5, 6} using the roster method, or Set A = {x |x is an integer ≥3 and ≤6} using the description method. In symbol form {x| x I ≥3 ≤6}.
One-to-One Correspondence and Cardinality
Sets are equal if they contain exactly the same elements. They are equivalent if they have the same number of elements. If each member of one set can be paired with only one member of another set, they are in one-to-one correspondence. The members do not have to equal one another, but the sets have to be equivalent, the same size. This is the basic idea behind counting, as one and only one number is paired with exactly one object. The sets have the same cardinality. Some sets are finite, such as Set A or the players on the active list of the Seattle Seahawks. Other sets are infinite, such as the set of integers I or Z, the set of whole numbers W, the set of rational numbers Q, real numbers R, and complex numbers C. A mathematician named Georg Cantor showed using one-to-one correspondence that the cardinality of infinite sets differed, so that there are levels of infinity. He designated the lowest level of infinity as א0, a level that is shared by the sets of integers, the sets of odd numbers, and the sets of even numbers. There are even more real numbers, and even more complex numbers, in higher levels of infinity, א1 and beyond.
Figure 1: Georg Cantor theorized that there were different levels of infinity.
Subsets
If an element is a member of a set, the symbol for that relationship is ∈. For example, {Marshawn Lynch ∈ Seattle Seahawks}. If an element is not a member of a set, the symbol for that relationship is ∉, so that {Peyton Manning ∉ Seattle Seahawks}. Suppose set B consists of the numbers {1, 2, 3, 4, 5, 6}. Set C consists of the numbers {2, 4, 6}. In this case, C is a subset of B, because all the numbers in Set C are in set B. In symbol form, C⊂ B. If Set D contains the number {7}, it is nowhere in set B, so D⊄B. The empty set has no elements in it. By definition, the empty set is a subset of all sets.
Figure 2: Using set language to describe a relationship between an element of a set and the entire set.
Venn Diagrams
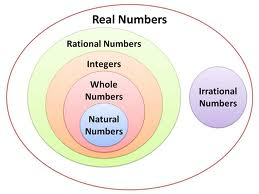
Relationships between different sets are shown with Venn Diagrams. If one set is a complete subset of another, so that all the members of one set are also members of another, the circle that represents the subset will be inside the circle that represents the larger set. If circles intersect, that means that both sets have some elements in common. If the sets have no common elements, the circles will be independent from each other.
Figure 3: The Venn diagram of the types of real numbers shows their relationship.
Interested in calculus tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Renton, WA: visit Tutoring in Renton, WA