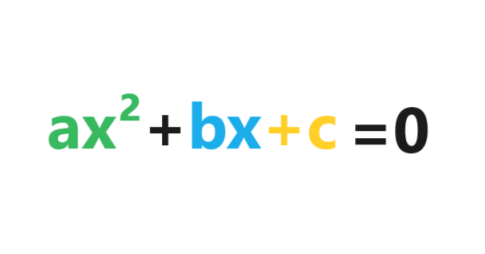Overview
A parabola is a graph of a quadratic equation. It is a U-shaped curve with an axis of symmetry. Many different objects in the real world follow the shape of a parabola, such as the path of a ball when it is thrown, the shape of the cables on a suspension bridge, and the trajectory of a comet around the sun. McDonald’s “Golden Arches” are two parabolas side by side.
Definition
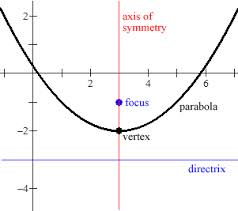
A parabola is defined geometrically by a point that is not part of its curve (called the focus) and a line that is not part of its curve (called the directrix). Every point of the parabola is the same distance (called equidistant) from the focus and the directrix. The axis of symmetry divides the parabola in half exactly and passes through the vertex. The parabola may open in any direction when it is graphed, either up, down, to the left or to the right.
Figure 1: This diagram of a parabola shows the focus, the directrix, and the axis of symmetry.
Conic Section
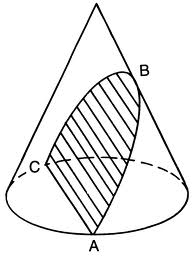
A parabola is one of the conic sections that is formed when a plane intersects with a cone as an open curve. If a cone is sliced so that the slice is parallel to the side of the cone, the slice is a parabola. It is a graph of a quadratic equation in the form ax2 +bx +c = 0, or an equation that can be simplified to that form.
Figure 2: Conic section showing a parabola.
Cliff Divers and Parabolas
The path of a cliff diver can be described by a quadratic equation similar to y = –x2 + 2x + 27. The trajectory of the diver is represented by a parabola, with y equal to the height above the water and x equal to the distance from the cliff. As the diver leaps off the cliff, the height above the water increases to the vertex of the parabola. As the diver gets closer to reaching the water, the height above the water decreases, but the distance from the cliff increases. Suppose that instead of a diver jumping off the cliff, a ball were thrown off the cliff into the water. Its path would also form a parabola.
Figure 3: The trajectory of the cliff driver follows a parabola.
Suspension Bridges
Parabolas are often found in architecture, especially in the cables of suspension bridges. This is because the stresses on the cables as the bridge is suspended from the top of the towers are most efficiently distributed along a parabola. The bridge can remain stable against the forces that act against it. Arches also follow a parabolic structure and are aesthetically pleasing.
Figure 4: The cables of suspension bridges follow the shape of a parabola.
Interested in geometry tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in San Francisco, CA: visit Tutoring in San Francisco, CA