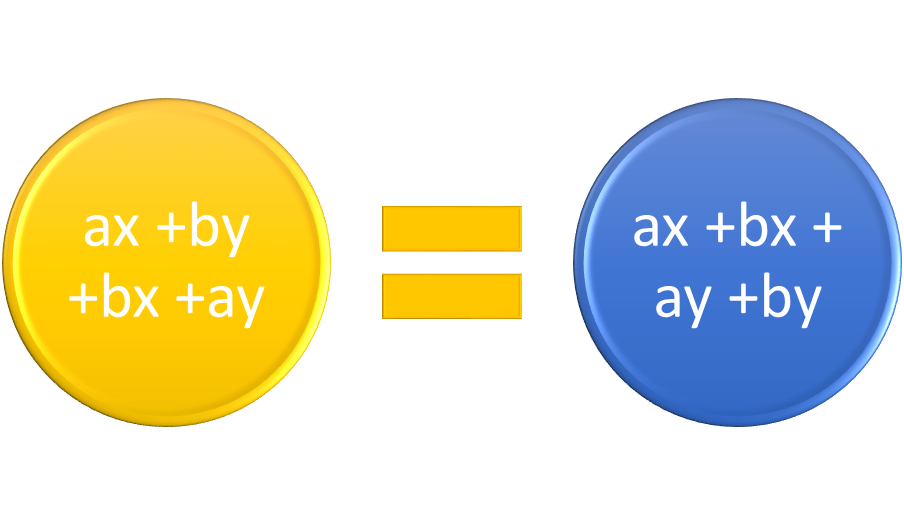Overview
Factoring by grouping is the best method to use when some terms in a polynomial share one common factor and some other terms in the same polynomial share another common factor. The common factors can then be factored out using the distributive property.
Determine the Common Factors
The first step is to determine if all the terms in a polynomial have a common factor. If they do, then the greatest common factor (GCF) can be factored. If they do not, determine if there are two terms in the polynomial that have one common factor and two other terms that have another common factor. Suppose the four-term polynomial is ax + bx + ay + by. Using the commutative property, it can be rearranged, so that ax and ay have the common factor a, and bx and by have the common factor b.
Figure 1: Rearranging terms in a polynomial using the commutative property.
Factor by Grouping
The first two terms, ax and ay, can be factored as a(x + y). The second two terms of the polynomial, bx and by, can be factored as b(x + y). The new polynomial is a(x + y) + b(x + y). Suppose the four-term polynomial is 5m + 2w + mw + 10. It can be rearranged so that 5m + 10 + mw + 2w, or 5(m + 2) + w (m + 2).
Figure 2: Factoring grouped terms
Factoring Negative Terms
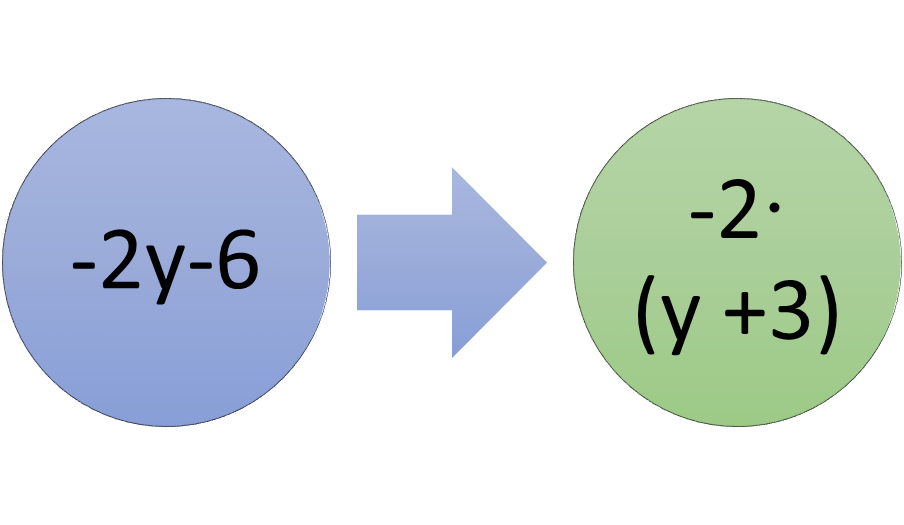
Suppose the polynomial were xy + 3x – 2y – 6. The first two terms can be factored as x(y + 3), and the second two terms can be -2(y + 3). When there is a negative term, the sign must be changed when it is multiplied, so that -2 times a positive 3 is -6. Similarly, suppose the polynomial were x2 – 3x + x -3. The first group, x2 – 3x, could be factored as x(x – 3). The second group, x -3, actually has one factor in common. The identity factor, 1, can be used, so that the second group can be factored as 1(x – 3).
Figure 3: When factoring negative terms, remember that signs change when multiplying.
Use the Distributive Property
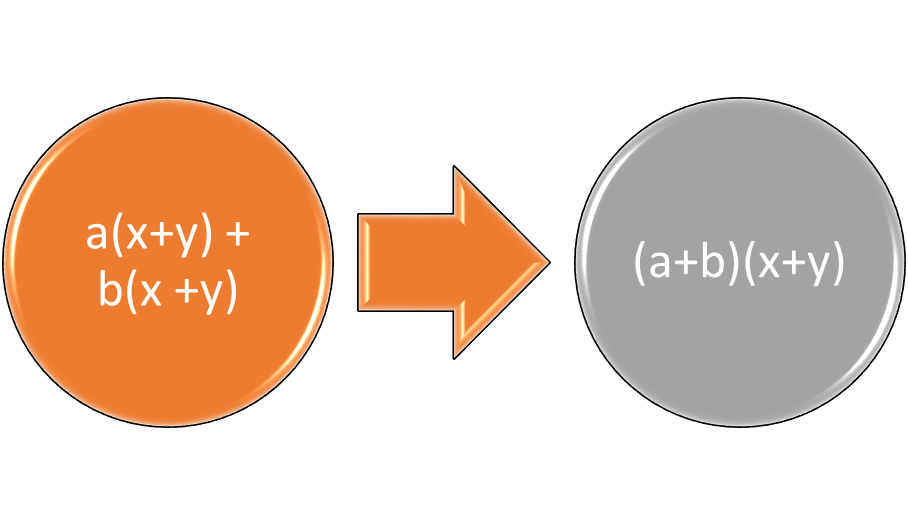
The polynomial in symbol form a(x + y) + b(x + y) can be factored using the distributive property as (a + b)(x +y). Similarly, the polynomial 5(m + 2) + w (m + 2) can be factored using the distributive property as (5 + w)(m + 2). The polynomial x (x -3 ) +1(x – 3) can be factored as (x + 1)(x – 3). The identity factor was used to illustrate the distributive property and factoring by grouping.
Figure 4: Use the distributive property after factoring by grouping.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Rayne, LA: visit Tutoring in Rayne, LA