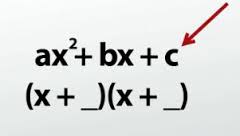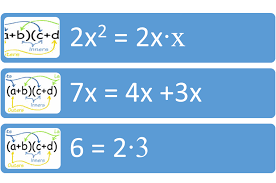Overview
Not all polynomial expressions are of the form x2 +ax +b, where the leading coefficient is equal to 1. Some polynomial expressions have a coefficient that is not equal to 1, and it must be factored also. However, the FOIL method can still be used, with one extra step to find the first product.
Factoring Trinomials
Suppose a polynomial expression is in the form of ax2 +bx +c, where a (the leading coefficient) is not equal to 1. That means that in order to factor the expression as (___x + ___) (___x +_____) the numbers in the first blanks will equal the coefficient a, the outside product and inside product can be added to equal the coefficient b, and the last blanks will have the product c.
The First and Last Products
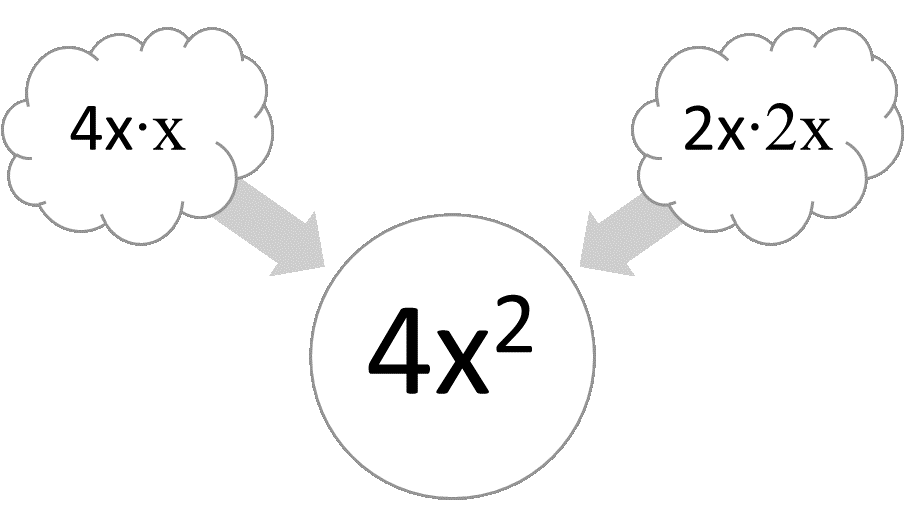
After checking to see if there aren’t any factors common to all terms, find the common factors for the leading coefficient a. Suppose the polynomial expression to factor is 6x2 +7x +2. The first term is 6x2, so in order to factor it, find the factors of 6x2. One pair is x, 6x, and another pair is 2x, 3x. Next find the factors of the last term 2. Because the number 2 is positive, the factors will either be both positive, 1 and 2, or both negative, -1 and -2.
The Middle Products
Using the possible factors for the first and last terms, try all the possible combinations: (x +1) (6x +2); (x +2) (6x +1); (3x +1) (2x +2); and (2x +1) (3x +2). Since the first and last terms have already been factored, it is a matter of finding the correct combination of middle products. For the first combination (x +1) (6x +2) the outer product is 2x and the inner product is 6x, equaling 8x. For the second combination, (x +2) (6x +1), the outer product is x and the inner product is 12x, equaling 13x. The third combination, (3x +1) (2x +2), the outer product is 6x and the inner product is 2x, equaling 8x again. The fourth combination, (2x +1) (3x +2), the outer product is 4x and the inner product is 3x, equaling 7x, the correct factorization.
Factoring Common Products
Sometimes, all terms in a polynomial have a common factor which must be factored out before the rest of the polynomial can be factored. Suppose the polynomial is 8m2 +8m -6. Each term has a common factor 2(4m2 +4m -3). Next, see if (4m2 +4m -3) can be factored further. The factorizations of 4m2 are 1m, 4m; 2m, 2m; and the factorizations of -3 are -1, 3; and 1, -3, since the factors of a negative number do not have the same sign. Again, it is a matter of finding the possible combinations and trying out the products (m-1) (4m +3); (4m-1) (m +3); (m+1) (4m -3); (4m +1) (m-3); (2m -1) (2m + 3); and (2m +1) (2m-3). The first combination, (m-1) (4m +3) equals 4m2 –m -3. The second, (4m-1) (m +3), equals 4m2-11m -3. The third (2m +1) (2m -3) equals 4m2 -4m -3. The fourth, (2m-1) (2m +3), equals 4m2 +4m -3. The correct factorization of 8m2 +8m -6 is 2(2m-1) (2m+3).
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Ann Arbor, MI: visit: Tutoring in Ann Arbor, MI