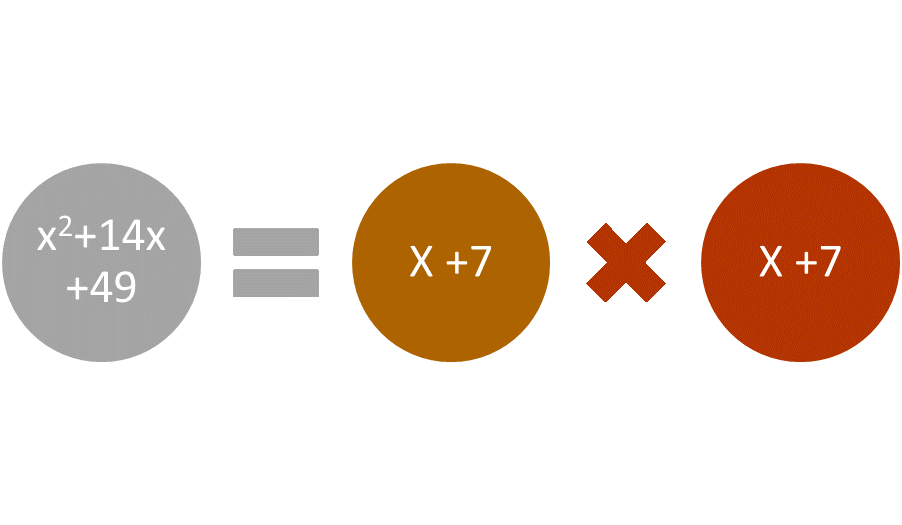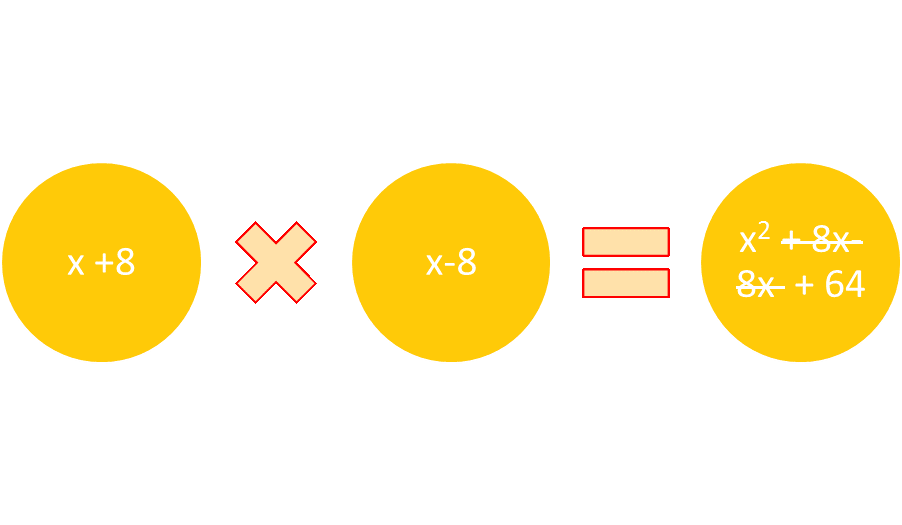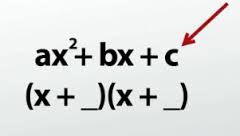Overview
Many quadratic trinomials follow a pattern that can be used to factor them. These patterns include the patterns for perfect square trinomials, the pattern for the difference of squares, and the pattern for using the properties of algebra.
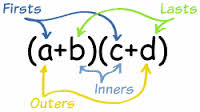
FOIL
All the patterns for factoring quadratic trinomials use the FOIL method of multiplying binomials. FOIL is an acronym for First, Outside, Inside, Last. Suppose the binominals to be multiplied are (x + 3) (x + 2). In both phrases, the variables are first, and x times x is x2. The furthest outside terms are 2x, and the closest inside terms are 3x. The last terms are 2 ∙ 3, which equals 6. The entire trinomial multiplied is x2 + 5x + 6.
Figure 1: The FOIL pattern of multiplying binomials.
Perfect Square Trinomials
Perfect Square Trinomials follow a pattern. The product of (a + b) (a + b) equals a2 + 2ab + b2. It also uses FOIL, as a is the first term, and a∙a equals a2. The variables b∙a are the outside term, and a∙b the inside term, equaling 2ab. The last term, b∙b, equals b2. A variant of this pattern is the product of (a-b)(a-b). It follows the pattern a2 -2ab + b2. Adding –ba and –ab equals -2ab, and the product of –b ∙-b is positive.
Figure 2: Factoring perfect square trinomials.
Difference of Squares
Multiplying the binomials (a + b) and (a – b) also follows a pattern. The product of a∙a is a2. The outside terms, -ab, and the inside terms +ba cancel each other out. The product of b∙-b is –b2, because a negative times a positive is a negative product. The pattern (a + b)(a – b) equals a2 – b2. Suppose the trinomial is x2 – 64. The middle term is understood as 0x, which is not necessary. Both x2 and -64 can be factored as x∙x and 8 ∙ -8, and the middle terms 8x and -8x cancel each other out.
Figure 3: When multiplying the difference of squares, the middle terms cancel each other out.
Algebraic Patterns
Some trinomials that are not perfect squares or the difference of squares also follow patterns so that they are easily factored. Whenever the squared term doesn’t have a coefficient, so that it actually means 1x2, it is always a good check to see if the trinomial can be factored. The variable x2 can be factored as (x + _) (x + _). The constants that fill in the blanks will be two numbers that their product is the last term and their sum is the sum of the outside and inside, following the FOIL pattern. Suppose that the expression is y2 -6y – 7. The coefficient of y2 is 1, so the pattern (y + _) (y + _) is worth trying. The numbers 1 and -7 and -1 and 7 are factors of -7. The sum of -1 and 7 is 6, and the sum of 1 and -7 is -6. The trinomial y2 – 6y – 7 is not a perfect square, but it can be factored as (y + 1)(y – 7).
Figure 4: The general pattern to factor trinomials.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Wheeling, WV: visit Tutoring in Wheeling, WV