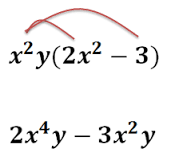Math Review of Multiplying Monomials and Binomials

Overview

Multiplying a binomial by a monomial follows certain rules, using the distributive and associative properties.  Multiplying a binomial by another binomial follows similar rules, and leads to the FOIL shortcut.

Multiplying Monomials

Remember that monomials can be multiplied by using the properties of rational numbers and the properties of exponents.  For example, the monomials 3x and 4x can be multiplied by using the associative and commutative properties of multiplication such that (3·4) (x·x), so that 3·4 equals 12, x·x equals x², or 12x².

Multiplying a Monomial by a Binomial

Multiplying a monomial by a binomial is similar, as it uses the rules for multiplying monomials, along with the distributive property.  For example, the binomial 2x +4 can be multiplied by the monomial 4x so that (2x) (4x) equals 8x² and 4·4x equals 16x, using the distributive property.  Therefore, (2x +4) (4x) equals 8x² + 16x.  Also, 5x (8y⁴-4x²-9y-11) equals 40xy⁴-20x³-45xy -55x.

Multiplying Two Binomials

Multiplying a binomial by a binomial is also similar, as it uses the distributive property twice.  For example, (x +3) (x+4) can be expanded using the distributive property once to x(x +4) +3(x +4) and again to x² + 4x +3x +12, or x² +7x +12.  Also, (x +3) (x-5) can be expanded to x(x-5) + 3(x-5) to x² -5x + 3x -15, or x² -2x-15.

Using FOIL

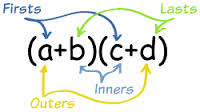
There is a shortcut to multiplying two binomials, so it is not necessary to remember to use the distributive property twice.  The process is to multiply the first terms of each binomial, the outside terms of each binomial, the inside terms of each binomial, and the last terms of each binomial, or FOIL.  Then collect the like terms by adding the outside terms.  It gives the same result as using the distributive property twice.  For example, (2x² -3) (x-2) can be multiplied by using the distributive property twice as 2x² (x-2) -3(x-2) or 2x³-4x^{2 –}3x +6.  It can also be multiplied by using FOIL, so that the first terms (2x²)(x) or 2x³, the outside terms (2x²)(-2) or -4x², the inside terms (-3)(x) or -3x, and the last terms, (-3)(-2) or 6.

Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.

SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Fayetteville, AR: visit:  Tutoring in Fayetteville, AR