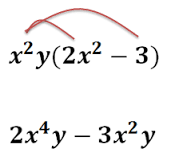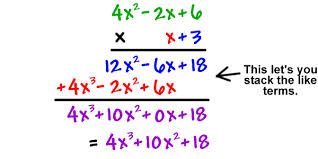Overview
Multiplying two polynomials is similar to multiplying a polynomial by a monomial, or multiplying a binomial by another binomial. It uses the same principle of multiplying each term by every other term.
Multiplying a Polynomial by a Monomial
Remember when multiplying a polynomial by a monomial to multiply each term of the binomial by using the distributive property. Then like terms can be combined. For example, 4x2(-2x3 + 5x2 + 10) means the same thing as (4x2) (-2x3) + (4x2) (5x2) + (4x2) (10) or -8x5 + 20x4 + 40x2. Notice that multiplying each term uses the rules of multiplying numerical coefficients, such as 4·-2 equals -8, 4·5 equals 20, and 4·10 equals 40. Multiplying each term also uses the rule of multiplying exponents.
Special Products of Binomials
When multiplying binomials, each term of one binomial must be also multiplied by each term of the other binomial. The distributive property is also used and like terms can be combined. For special binomials, shortcuts can speed the process. For example, any binomial (A + B) 2 equals A2 + 2AB + B2, and any binomial (A-B) 2 equals A2– 2AB + B2. Similarly, (A + B) (A-B), also known as the sum and difference of two binomials, always equals A2 – B2.
Using FOIL
Any two binomials, whether they are special products or not can be multiplied by using the acronym FOIL, as a mnemonic to ensure all terms in one binomial are being multiplied by all terms in the other binomial. Using FOIL, the first terms are multiplied, the outer terms, the inner terms, and the last terms. Then like terms are combined. For example, when multiplying (x +5)(x +6), the first terms are x·x, or x2. The outer terms are 6·x, or 6x, and the inner terms are 5·x, or 5x. Then, 5x and 6x are like terms and can be added, as 11x. Finally the last terms, 5·6, or 30 can be combined. The entire equation is (x +5) (x +6) equals x2 +11x +30.
Multiplying Polynomials
Multiplying polynomials is similar to multiplying monomials and binomials, except that every term in one polynomial is multiplied by every other term in the other polynomial. Suppose the equation is (x2 + 2x +3) (4x +5). Start by multiplying x2 by 4x, or 4x3, then x2 by 5 or 5x2. Next, 2x by 4x or 8x2. Next 3 by 4x gives 12x and 3 times 5 is 15. That leaves 4x3 + 5x2 + 8x2 + 12x + 15. Finally, combine like terms, since 5x2 +8x2 equals 13x2, so that the equation in simplest terms is 4x3 + 13x2 + 12x +15.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Marietta, GA: visit: Tutoring in Marietta, GA