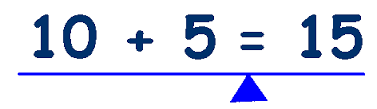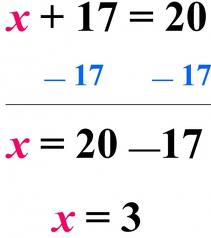Overview
Some algebra equations can be solved with one step, using operations such as addition, subtraction, multiplication, and division. In order to solve them, use inverse operations so that the variable is on one side and real numbers are on the other side. Then, solve the problem with arithmetic.
Balanced Equations
An equation is solved when both the left side of the equation and the right side of the equation mean the same thing. Take a math fact such as 2 + 3 = 5. It is true for real numbers because 2 + 3 equals 5, and 5 equals 5. Suppose the equation were 3 +7 =x. In order for the equation to be balanced on both sides, x = 10, because 3 +7 equals 10 and 10 equals 10.
Inverse Operations
Addition and subtraction are inverse operations; and multiplication and division are inverse operations. That is because adding a number and its inverse equal the additive identity, or zero; and multiplying a number by its inverse equal the multiplicative identity or 1. In math symbol language a – a =0, and a/a, as long as a doesn’t equal zero, is 1. Adding or subtracting zero doesn’t change anything, and multiplying or dividing by 1 doesn’t change anything. The equation stays balanced by using the inverse on both sides.
Solving Problems by Adding or Subtracting
An equation such as 12.5 +7.2 = x is easy to solve because the variable x is already on one side and the real numbers (also called constants) are on the other. By adding up the constants, 12.5 + 7.2 = 19.7, so x equals 19.7. Suppose the equation were 2 + x = 5. Keep the equation balanced by using the same inverse on both sides. Since it is an addition problem, the inverse of addition is subtraction. In this example, 2 -2 +x = 5 -2, or 0 + x = 5-2, or x =3. Similarly, y -3 = 10 remains balanced when y – 3 +3=10 +3, or y +0 = 10 +3, or y = 13. The equation is a subtraction problem, and the inverse of subtraction is addition.
Solving Problems by Multiplying or Dividing
In an equation such as 4·11 = z, z equals 44. The constants are already on the left side and the variable is already on the right side of the equation. Suppose the equation were 9x =72. In that case, it is a multiplication problem, and the inverse of multiplication is division. 9 ·1/9·x = 72 ·1/9, because 9 ·1/9 ·x = 1x, or x, and 72/9 = 8, so x = 8. Similarly, x/3 = 12 becomes 3 ·1/3 ·x = 12·3 or x = 36.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Moncton, NB: visit: Tutoring in Moncton, NB