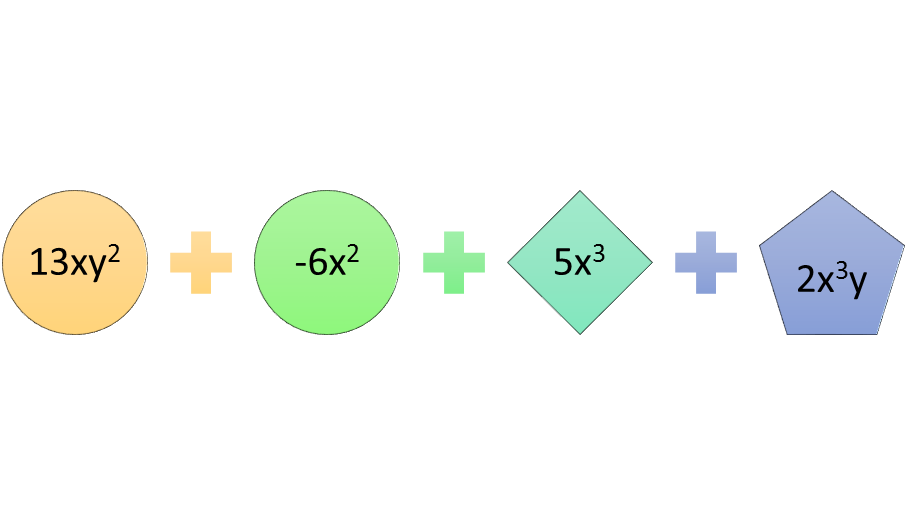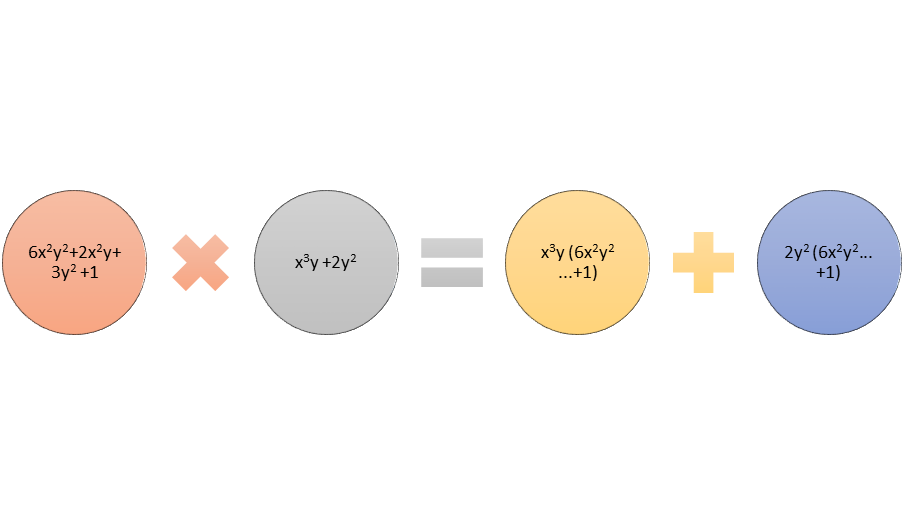Math Review of Operations with Polynomials with More than One Variable

Overview

Polynomials with more than one variable are often used in applications when one variable has a relationship with another. Special attention to combining like terms is essential to solving them correctly.

Combining Like Terms

The expressions that contain like terms have exactly the same variables with the same exponents. For example, 3x²y⁴ can be combined with x²y⁴. Similarly, 9yz² can be combined with -2yz². However, 10xy² cannot be combined with 5x²y. Although the variables are the same in both monomials, the degrees of the variables are not. Similarly, 8xy cannot be combined with 3yz, because both terms do not have the same variables.

Figure 1: Terms can be combined if they are like terms, but must stand alone if they are unlike terms.

Addition

In order to add polynomials with more than one variable, add all the terms and then combine like terms. Suppose that 5xy² – 4x²y + 5x³ + 7 is added to 8xy² – 2x²y + 2x³y + 10. The sum will equal 5xy² + 8xy² – 4x²y – 2x²y + 5x³ + 2x³y + 7 + 10. The like terms 5xy² and 8xy² can be combined as 13xy². The like terms -4x²y and -2x²y can be combined as -6x²y, and the like terms 7 + 10 can be combined as 17. The unlike terms 5x³ and 2x³y are part of the sum. The entire sum is 13xy²-6x²y + 5x³ +2x³y + 17.

Figure 2:  In the final sum or difference, like terms are combined and unlike terms are separate.

Subtraction

In order to subtract polynomials with more than one variable, the additive inverse of the polynomial is added. This means that every term of the polynomial to be subtracted has an opposite sign. Suppose that the expression is (5x³y² – 3x²y + 4yz + 8z² + 9) – (3x³y – x²y + 12z³ + 2z² – 1). The additive inverse is -3x³y + x²y -12z³ – 2z² + 1. Combining like terms, -3x²y + x²y is -2x²y, 8z² – 2z² is 6z², and 9 + 1 is 10. There are a number of unlike terms, so the entire difference is 5x³y²-3x³y – 2x²y + 4yz – 12z³ + 6z² + 10.

Multiplication

Polynomials with more than one variable are multiplied similar to polynomials with one variable, in that every term in one polynomial is multiplied by every term in the other polynomial. Suppose that (6x²y² + 2x²y + 3xy + 1) is multiplied by (x³y + 2y²). The first term, (6x²y² + 2x²y + 3xy + 1) (x³y), using the rules of exponents, is 6x⁵y³ + 2x⁵y² + 3x⁴y² + x³y. The second term, (6x²y² + 2x²y + 3xy + 1) (2y²), also using the rules of exponents, is 12x²y⁴ + 4x²y³ + 6xy³ + 2y². If there were like terms, they would be combined. The entire product is 6x⁵y³ + 2x⁵y² + 3x⁴y² + x³y + 12x²y⁴ + 4x²y³ + 6xy³ + 2y².

Figure 3: Every term in one polynomial is multiplied by every term in the other polynomial.

Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.

SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Golden, CO: visit Tutoring in Golden, CO