Overview
Operations with sets include the union of sets, the intersection of sets, and complements of sets. These operations can be applied to solve survey problems using sets.
Special Types of Sets
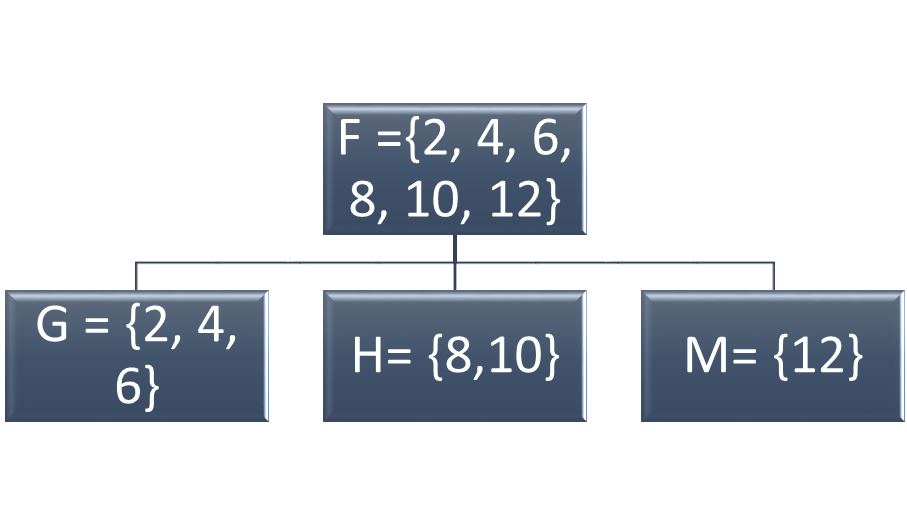
Some special types of sets include the null or empty set, the universal set, and proper and improper subsets. The null or empty set ⦰ has no elements. Its set notation is { }. In contrast, the universal set U contains all the members of every set in an operation. While the empty set is always the same, a set with no elements, the universal set changes with each problem. It is defined before any operations take place. Suppose that set F is the universal set for a problem. It contains the elements {2, 4, 6, 8, 10, 12}. Therefore, all operations on set F will contain only those elements. Proper subsets of Set F will include some of the elements of Set F, such as Set G {2, 4, 6} or Set H {8, 10}. In set language, the symbol shorthand is G ⊂ F. Improper subsets of Set F will contain all the members of Set F. Set I {12, 10, 8, 6, 4, 2} is an improper subset of Set F.
Figure 1: Set F is the universal set for this problem; Sets G, H, and M are proper subsets.
Union and Intersection of Sets
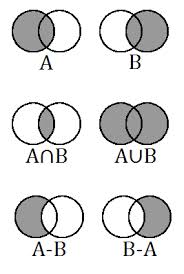
The union of sets is designated by the symbol ⋃, so if Set G {2,4,6} and Set H {8, 10} G ⋃ H = {2, 4, 6, 8, 10}. The intersection of sets consists of the elements that two or more sets have in common. Suppose that Set J {1, 2, 3,4, 5} and Set K {a, 3, d, 4, q}. The intersection of sets J⋂K is {3, 4}. Those are the only points common to sets J and K.
Figure 2: Venn diagrams as operational definitions of sets and operations.
Complements of Sets
The complement of a set is in relation to the universal set for that problem. Remember the universal set F with the elements {2, 4, 6, 8, 10, 12}? If Set O {6, 8, 10}, the complement of O (Ō), is {2, 4, 12}. If the universal set for a problem is I, the set of integers, and set L is {1, 3, 5, 7 …} the complement of L will be {0, 2, 4, 6 …}.
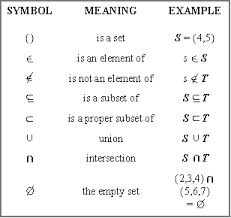
Figure 3: Some symbols and terminology of sets.
Solving Survey Problems with Sets
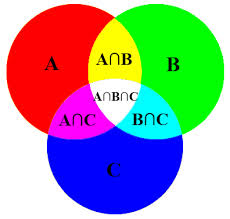
Suppose that 100 people are asked what types of shows they like to watch on TV. Suppose that 15 watch sports, 15 watch mysteries and true crime, 12 watch reality TV, 20 watch reality TV and mysteries, 28 watch sports and mysteries, and 3 watch sports, mysteries, and reality TV. How many people watch neither sports, mysteries, nor reality TV? This can be solved by using a Venn diagram and logic. Let Set S equal sports, Set M equal mysteries, and Set R equal reality TV. The intersection of S⋂M⋂R is 3, so the complement will be 15 -3 or 12. In other words, there are 12 others of the people who watch sports. Some of them watch only sports, some of them watch sports and mysteries, and some of them watch sports and reality TV. We already know that there are 15 people who watch mysteries, but some of them also watch sports, and some of them also watch reality TV. Similarly, the intersection of S⋂M⋂R is 3, so the complement will be 15 -3 or 12. There are 12 people who watch reality TV, but 3 of them also watch sports and mysteries, so the complement of 12-3 equals 9. The part of Set M that is not part of Set S is (15 – 3) or 12, and the part of Set M that is not part of set R is 12 -3 or 9. Finally, the part of Set R that is not part of Set S is 15 -9 or 6. 15 + 9 + 3 = 27. 100 – 27 = 73, or 73 people watch neither sports, mysteries, nor reality TV.
Figure 4: Venn diagram showing regions and relationships of 3 different sets.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Lynchburg, VA: visit Tutoring in Lynchburg, VA