Overview
Solving application problems is a process that includes understanding the problem, translating it into an equation, solving the equation, checking the answer, and answering the question. This process can be used to solve many different types of problems.
Understanding and Setting up The Application Problem
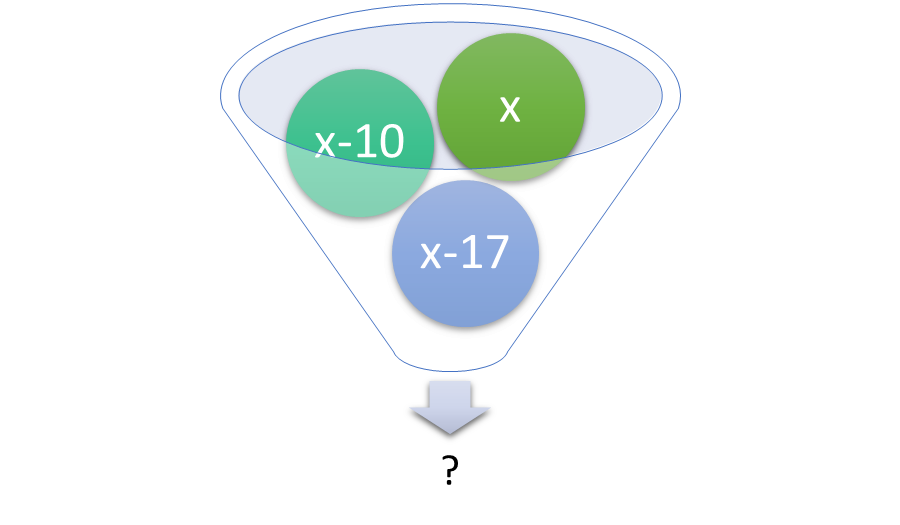
The first part of the process involves understanding what is being asked. This includes noticing any key words that refer to operations and any quantities that are in relationship to one another. It is important to have an idea of what sort of quantity will represent a solution. Suppose a problem asks how many points the first-place winner had. That would require just one answer. If the problem described that the first-place winner had 10 points more than the second-place winner, and 17 points more than the third-place winner, all three point values would be necessary to completely answer the question.
Figure 1: Setting up the application problem involves finding quantities in relationship to one another.
Translating the Problem into an Equation
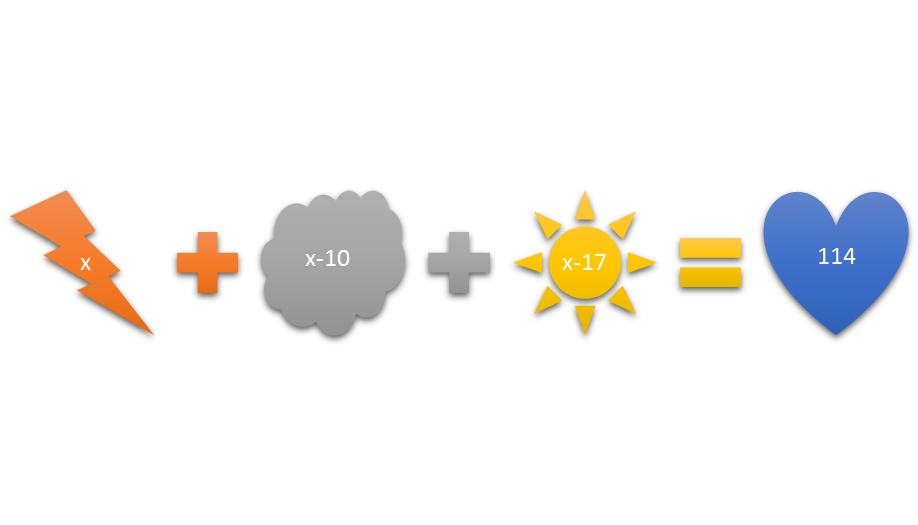
The second part of the problem involves putting the problem in symbol form. This includes choosing a letter to represent a variable, and writing down exactly what the variable stands for. Suppose that the point values of the three winners totaled 114. Let the point value of the first-place winner be x, the second-place winner x – 10, and the third-place winner x – 17. Then, x + x – 10 + x – 17 = 114.
Figure 2: Translating the problem into an equation involves putting the problem into symbol form.
Solving and Checking the Equation
If x + x – 10 + x – 17 = 114, then 3x = 114 + 27, or 3x = 141. So, x = 47, x – 10 = 37, and x -17 = 30. To check, 47 + 37 + 30 = 114. The answer makes sense, and fits the parameters of the problem. In this case, the original equation was x + x -10 + x – 17 = 114.
Answer the Question Asked
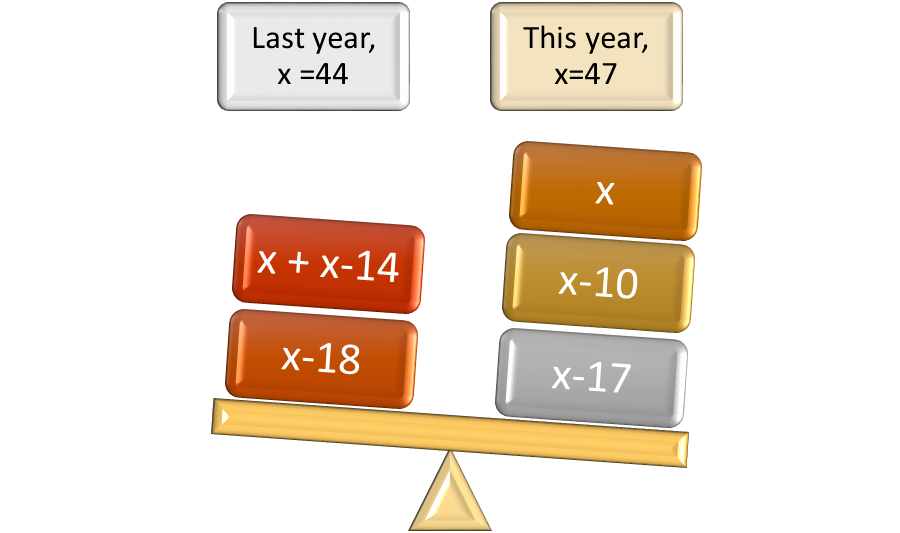
If the work is done to understand the problem before it is set up and solved, it is easier to answer the appropriate question. In this case, all three point values were necessary to completely answer the question. Suppose that more information were added to the problem. During the same contest last year, the point values of the first-place, second-place and third-place winners totaled 100, but the second place winner had 14 points less than the first-place winner, and the third-place winner had 18 points less than the first place winner. Which year did the third-place winner earn more points, and what was the difference? Last year, the equation was x + x – 14 + x – 18 = 100, so 3x = 132. The first-place winner earned 44 points, the second-place winner earned 44-14 or 30 points, and the third-place winner earned 28 points. However, the question asked has 2 parts. Last year, the third-place winner earned 28 points, and this year, the third-place winner earned 30 points. This year, the third-place winner earned more points, and the difference was a gain of 2 points.
Figure 3: Answering the question asked brings all the parts of the problem into balance.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Lenexa, KS: visit Tutoring in Lenexa, KS