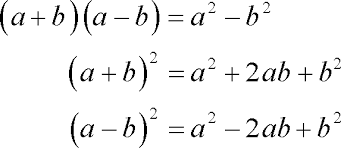Overview
The FOIL Method is a shortcut to multiplying binomials, rather than using the distributive property twice. Some special products of binomials suggest other patterns, such as the product of the sum and difference of two expressions, the product of squaring the sum of an expression, and the product of squaring the difference of an expression.
Review of FOIL
FOIL is an acronym for the order of multiplying terms in a product of two binomials. Suppose the binomials were (x +2) (x +3). The first step is to multiply the first terms, x·x or x2. Next, the outside terms, 3x, and then the inside terms, 2x. Finally, the last terms, 2·3, or 6. Combining like terms, the product of (x + 2) (x +3) equals x2 +5x +6.
Sum and Difference
The product of the sum and difference of two binomials can be expressed in algebraic terms as (a +b) (a-b). Using FOIL, the first step is a2, followed by the outside step –ba, followed by the inside step, ab, followed by the last step, b2. The outside –ba and the inside ab cancel each other out, so combining like terms leaves (a +b) (a-b) equaling a2 +b2. For example, (x +4) (x-4) equals x2 -4x +4x +16 or x2 – 16.
Squaring the Sum
Suppose each binomial is the same expression, such as (x +y) (x +y). Using FOIL, the first step is x2, followed by the outside step xy, followed by the inside step yx , followed by the last , y2. Combining like terms, x2 +2xy +y2 is the result. For example, (x +5) (x +5) equals x2 +5x +5x +25, or x2 +10x +25. Both x and 5 are squared, and the product of 5x is doubled for the middle term, rather than cancelling each other out, as in the product of the sum and difference.
Squaring the Difference
Suppose that each binomial is a difference rather than a sum, so that the product is (x-y) (x-y). In that case, the first term, x2, is the same. The last term, y2, is also the same, because –y ·-y is y2. The product of two negative numbers is a positive number. The outside term is –xy and the inside term is –yx, which add to form -2xy. Only the sign of the middle combination has changed. For example, (x-6) (x-6) is x2 -12x +36.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Grass Valley, CA: visit: Tutoring in Grass Valley, CA