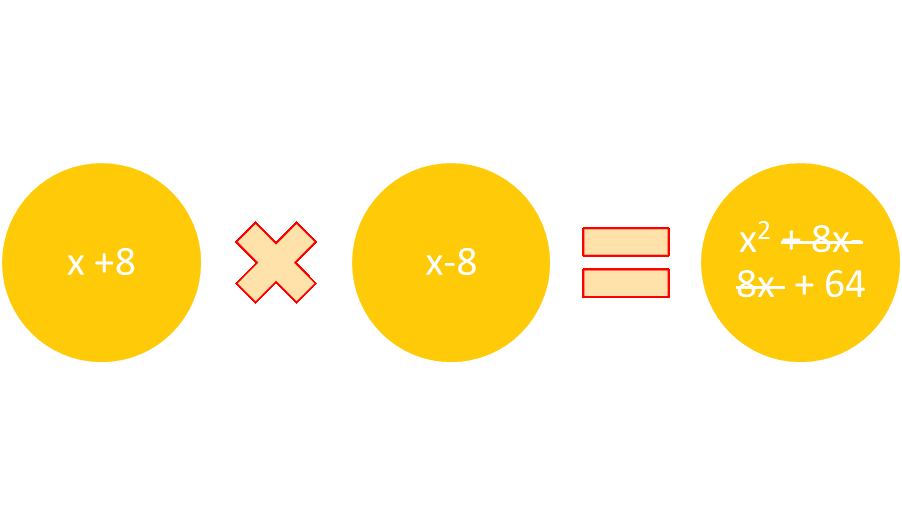Overview
As a general strategy for factoring polynomials, first check to see if there are any common factors. If there are not, check for the number of terms. If there are two terms, it may be a difference of squares. If there are three terms, it may be a perfect square of a binomial, or it may be possible to factor using a pattern. If there are four terms, it may be possible to factor by grouping.
Difference of Squares
An expression such as x2 – 36 follows a common pattern, as both x2 and 36 are perfect squares. Recall that they can be factored as (x +6) (x -6), as the middle terms, 6x and -6x, cancel each other out. What about an expression such as 10x3 – 40x? First, factor out the common factor 10x(x2 – 4) because 10x ·x2 is 10x3 and 10x·4 is 40x. The expression x2 -4 follows the pattern of a difference of squares, as (x+4) (x-4), so the entire factorization of 10x3 – 40x is 10x(x +4) (x-4). It is factored completely.
Perfect Square of a Binomial
An expression such as x6 + 8x3 +16, also follows a common pattern. The first term, x6, can be factored as a perfect square, x3·x3. Similarly, the last term, 16, can be factored as a perfect square, 4·4. The middle term, 8x3, is 4x3 + 4x3, so the expression x6 + 8x3 +16 can be factored as (x3 +4) (x3 +4). Recall the pattern of the perfect square of a binomial (a2 +2ab + b2) equals (a + b) (a +b).
Factor Using a Pattern
Not all trinomials are perfect squares of a binomial. Some trinomials have a leading coefficient of 1, and they will factor as (x + __) (x + ___). Other trinomials have a leading coefficient of (__x + __) (___x + ___). Suppose the expression is 5x2 + 15x +10. Each term has a common factor of 5(x2 +3x + 2) which can be factored further as 5(x +1) (x +2).
Factor Four Terms by Grouping
Some expressions with four terms can be factored by grouping, just as trinomials can. For example, 6x3 -9x2 + 4x -6 can be factored by factoring each group. 6x3 -9x2 can be factored as 3x2 (2x -3), and 4x -6 can be factored as 2(2x -3). The two groups can be combined as (2x -3) (3x2 +2).
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Duluth, MN: visit: Tutoring in Duluth, MN