Overview
Linear equations can form a system if two or more equations contain the same linear variables. A solution to a system of linear equations must be correct for both equations in the system. If a value solves one equation in the system but not the other, it is not a solution.
Is It a Solution?
A particular ordered pair can be tested within each equation in a linear system to see if it is a solution to the equations in the system. Suppose the ordered pair is (1, 3) and the equations in the system are 2x + y = 5 and -2x + y = 1. In the first equation, 2(1) is 2 and 2 + 3 = 5, so (1, 3) is a solution of the first equation. In the second equation, -2(1) is -2 + 3 is 1, so (1, 3) is a solution of the second equation, thus a solution of the system. Suppose the ordered pair is (2, -1) and the equations are x -2y = 4 and 3x +y = 6. In the first equation 2 – 2(-1) = 2 +2 = 4, so the ordered pair (2, -1) is a solution of the first equation. In the second equation 3(2) is 6 -1 is equal to 5, not to 6. The ordered pair (2, -1) is not a solution of the system, because it doesn’t solve both systems.
Graphing Systems of Linear Equations
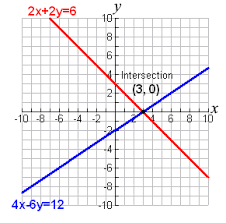
If a system of linear equations has one solution, the graph of each linear equation in the system will intersect at only one point. Suppose the equations are 2x + 2y = 6 and 4x – 6y = 12. They appear from the graph to have one solution, the ordered pair (3, 0). However, the only way to see if that solution is correct is to substitute the ordered pair in each equation to determine if it is a solution of the system. In the first equation, 2(3) + 2(0) = 6, so the ordered pair is a solution. In the second equation, 4(3) -6(0) is 12, so that ordered pair (3, 0) is a solution of the system.
What If All Solutions Are Correct?
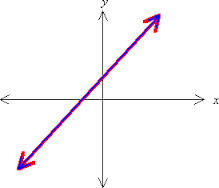
Sometimes a system of linear equations has more than one correct solution. The only time a linear system can have all solutions in common is if each linear equation is the same line. The solutions are infinitely many, because any solution of one equation is also a solution of the other equation. For example, a system of equations such as 2x – y = 3 and 4x – 2y = 6 both cover the same line.
What If No Solutions Are Correct?
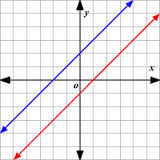
Some systems of linear equations have no solutions in common. If two lines have the same slope but different y intercepts, they will graph as parallel lines. They can be graphed as a system of linear equations, because they have the same variables, but any solution for one linear equation will not be a solution for the other linear equation.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Alamo, TX: visit: Tutoring in Alamo, TX