Mean, Median, and Mode

Broadly speaking, statistics is a tool that allows us to describe and compare large amounts of information in a digestible way. Some of the most basic, as well as most useful metrics when analyzing a dataset or distribution are the mean, median, and mode. Let’s take some time to define each of these terms, use them in examples, and describe situations where they may be useful.

Mean

Often referred to as the average, the mean of a dataset is the sum of values of a dataset divided by the number of values in a dataset. Mathematically, this is often represented as:

   

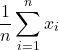
If that looks too complicated, don’t worry, it just means that we add all of our values in the dataset (the ‘s) and then divide by the number of values in the dataset ().

Example

Let’s look at an example. Suppose we have the following values from a dataset:

   

To compute the mean of these 7 values we do the following:

   

Application

We might now ask “why do we care about the mean?” Let’s answer that via an example. Suppose you are a baseball player trying to hit the fastball of a pitcher. To anticipate how to approach your at-bat, you look at how fast the pitcher throws their fastball. You look at the pitcher’s last 5 fastballs, which were 90 MPH, 91 MPH, 88 MPH, 93 MPH, and 89 MPH. You could calculate the average speed of these pitches (90.2 MPH) to predict how much time you have to react to that pitcher’s fastball. A useful tool indeed!

Median

Next, we will consider the median of a dataset. The median is simpler to calculate than the mean. We simply sort the values in a dataset from least to greatest and choose the middle one as our mean. If there are an even number of values in the dataset, we simply find the mean of the middle two values.

Example

Let’s look at an example. Suppose we have the following values from a dataset:

   

First, we need to sort the values from least to greatest, giving:

   

This sorted dataset has 8 values, so we start by picking the middle two: 4 and 5. We then compute the mean of these two values to get 4.5 as the median of this dataset. You may notice that this is the same dataset as the one we used in the mean, but that the median and mean are different. Don’t worry, we will get back to that.

Application

The median of a dataset is similar to the mean of a dataset, except it is not affected by outliers: extreme values that can skew the mean. For example, let’s say you are analyzing the traffic speed on a highway. You observe the speeds of 5 cars: 55 MPH, 61 MPH, 58 MPH, 59 MPH, and 103 MPH(!). If we took the mean of this dataset we might predict that most cars are travelling at 67.2 MPH, but this is much higher than the speed that most cars are actually travelling. By choosing the median speed (59 MPH), we reduce the impact of the one car that is speeding and obtain a more realistic prediction for the speed of most cars.

Mode

The mode of a dataset is the least commonly used, but has some niche applications. It is simply the most commonly occurring value in a dataset. If there are multiple values that occur the same number of times, then there will be multiple modes.

Example

Let’s look at an example. Let’s return to the same dataset from our other examples:

   

The mode of this dataset is 1, as it occurs twice and all other values only occur once.

Application

The mode is most useful when data is expected to represent pre-defined categories. A good example is shirt sizes. It is difficult to conceptualize what the average shirt size is (what would a medium-and-a-half even mean?) and we know that the median shirt size will always be medium or large depending on the number of available sizes. This is where the mode is important. Perhaps we are a clothing store and we want to know what shirt size is most common. The 5 most recent customers purchased the following shirt sizes: M, M, L, M, XL. The mode of this dataset would be M, as it occurs 3 times. We can then predict that medium is the most common size and order shirts accordingly.

Comparison

The astute reader of this post will notice that we used the same distribution in an example of the mean, median, and mode. A natural question would be “how do I know which one to use?”. Unfortunately, there is no universal answer to this question, but we can suggest the following:

• If you want to make observations and predictions about a group and include extreme outliers, use the mean
• If outliers are not important to your conclusions, use the median
• If you are analyzing categories or binned (grouped) data, use the mode

This has been a brief introduction to the mean, median, and mode. For more information on this topic as well as assistance with homework and test preparation, feel free to reach out to an Academic Director toll-free at 1 (877) 545-7737 or via our Contact Us page.