What are Quadratic Equations?
The general form of quadratic equations is
![]()
where ![]() is our unknown
is our unknown ![]() are real numbers and
are real numbers and ![]() . The last statement is important as if
. The last statement is important as if ![]() was zero, the term
was zero, the term ![]() would be zero and the equation wouldn’t have a quadratic term.
would be zero and the equation wouldn’t have a quadratic term.
Having a quadratic term is not enough though, you cannot have your unknown to any power bigger than ![]() (i.e..
(i.e.. ![]() ,
, ![]() , etc.) and also the expression must be a polynomial (there cannot be “weird” functions like
, etc.) and also the expression must be a polynomial (there cannot be “weird” functions like ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() affecting our unknown) only non-negative integers are allowed.
affecting our unknown) only non-negative integers are allowed.
In practice, quadratic equations can take a lot of forms and look quite different than their general form. Let’s see some examples:
![]()
These are examples of equations which are not quadratic:
![]()
![]()
![]()
![]()
Now we put our attention on how to solve these equations.
Solving Quadratic Equations
General Form
While solving quadratic equations we must take into consideration their form. To know the form of a quadratic equation we can put it in general form (G.F). General Form is no more than the equation written as ![]() . Notice that all the terms are on the left of the equal sign in order (
. Notice that all the terms are on the left of the equal sign in order (![]() first and
first and ![]() second), and with zero on the right. Let’s see some examples of how to take a quadratic equation to G.F.
second), and with zero on the right. Let’s see some examples of how to take a quadratic equation to G.F.
![]()
![]()
![]()
Solving the Quadratic Equation
The following diagram describes how to solve a quadratic equation, once it is in General Form.
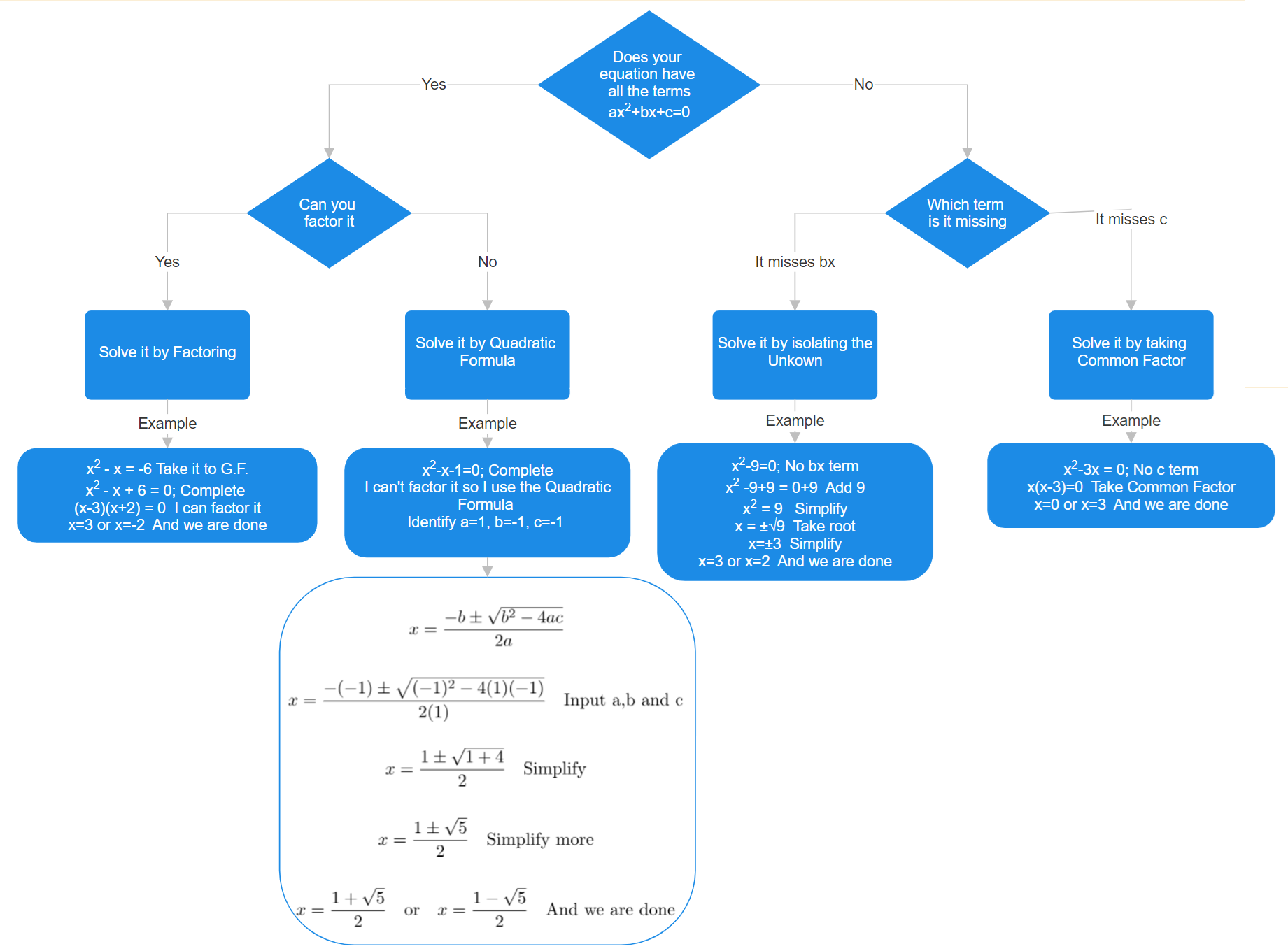
Factor if you can
If you thought that factoring was not useful, you are wrong. Factoring is essential to solving equations of any type, especially for quadratic equations. We can see why by remembering a key feature of numbers.
“If a multiplication of numbers equals zero, then one of the factors must be zero”
For example, if ![]() then one of them must be zero
then one of them must be zero ![]() ,
, ![]() or
or ![]() . Let’s see how to exploit this principle to solve equations.
. Let’s see how to exploit this principle to solve equations.
![]()
Notice that this is a multiplication that equals zero then that means that
![]()
Notice that both of the resulting equations are simple linear equations! And we know how to solve them, the results are:
![]()
These are precisely the solutions to our equation.
If you can’t factor use the Quadratic Formula
Factoring is not always easy or obvious. For those cases, or any case in fact, you always have the quadratic formula at your service. At last here it is:
The solution to an equation to the form ![]() is given by
is given by
![]()
The quadratic formula can solve any quadratic equation, but it can take a lot of steps to reach a solution. This means that you should use it only when it is necessary. We must accept the formula can look a bit scary at first. However, all you need to do is identify the values of a,b and c from your equation. Let’s solve ![]() using the quadratic equation.
using the quadratic equation.
First identify ![]() ,
,![]() and
and ![]()
![]()
Use them in the quadratic formula
![]()
Simplify

In this case, we have two solutions, one given by separating ![]() into plus and minus
into plus and minus

If you notice this is the same solution we found in the previous section (As we solved the same equation). I hope you agree that by factoring we solved the equation faster.
Special Cases
When the equation is missing terms, the linear term ![]() or the constant term
or the constant term ![]() . We can solve the equation easily.
. We can solve the equation easily.
Missing bx
When ![]() the equation looks like
the equation looks like ![]() . Examples are
. Examples are ![]() ,
, ![]() or
or ![]() .
.
To solve this equation we need only need to isolate ![]() (You could solve it by factoring or using the quadratic formula as well, but I think this is the easiest approach).
(You could solve it by factoring or using the quadratic formula as well, but I think this is the easiest approach).
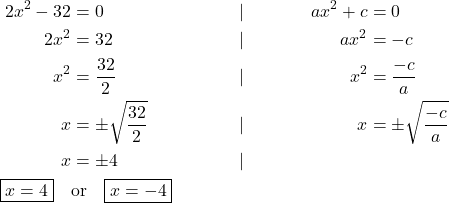
Missing c
When ![]() the equation looks like
the equation looks like ![]() . Examples are
. Examples are ![]() ,
, ![]() or
or ![]() .
.
To solve this equation we need only need to take the Common Factor (Factoring again!).

Notice that zero is always a solution for these types of equations.
No solutions for Quadratic Equations
Sometimes, a quadratic equation has no solutions in the real numbers. This happens whenever in one of our methods we encounter the square root of a negative number (i.e. ![]() ). If you are working in real numbers and you see one of these square roots your answer should be immediately:
). If you are working in real numbers and you see one of these square roots your answer should be immediately:
“There is no solution in the real numbers”
As a disclaimer, these equations have solutions in complex numbers, but that is a different topic that deserves its own post.
Solving Quadratic Equations Using Technology
Lastly, I want to show you how to solve a quadratic equation technology. You can use for example this widget from Wolfram Alpha.
If you need to write ![]() for example you can do so by writing “sqrt(2)” and exponents like
for example you can do so by writing “sqrt(2)” and exponents like ![]() can be written as 3^2.
can be written as 3^2.
Step-by-step solutions are available in Symbolab. Wolfram Alpha also has this option but it is paid.
Calculators and Quadratic Equations
Some calculators can solve quadratic equations as well. Check yours! You would be surprised by the power of your calculator. This video from Blackpenredpen has an example of how to solve a quadratic equation using a Casio calculator.
This has been a brief introduction to the concepts of quadratic equations. For more information on this topic as well as assistance with homework and test preparation, feel free to reach out to an Academic Director toll-free at 1 (877) 545-7737 or via our Contact Us page.
Powered by WordPress with QuickLaTeX