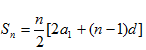An arithmetic sequence is a sequence in which the difference between consecutive terms is constant. A series is the indicated sum of all the terms in a sequence. An arithmetic series is the sum of an arithmetic sequence. Such as,
2 + 4 + 6 + 8 + 10
Since the difference is common to all consecutive pairs of terms, it is called the common difference, denoted by d.
d = an+1 – an
An arithmetic series a1 + a2 + a3+ a4 +…… + an can be expressed in the terms of first term a1 and the common difference d as below.
Sn = a1 + (a1 + d) + (a1 + 2d) + (a1 + 3d) +…..+ (a1 + (n – 1)d)
Sum of n terms of an arithmetic series is give as
General term of a an arithmetic series is as
an = a1 + (n – 1)d
Example:
2, 5, 8, 11, 14, 17, 20
a1 = 2
d = 5 – 2 = 3
n = 7
Sum, S7 = 7/2 × [2 ×2 + (7 – 1)3]
= 7/2 × (4 + 6 × 3)
= 7/2 × 22
= 7 × 11 = 77
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students, visit: SchoolTutoring Academy.