What is Slope?
Imagine you go to the store and want to buy your favourite chocolate. Your mom has given you 30 dollars to spend! Once you get there you notice that the price tag says 10 dollars each. You stop a second and wonder how many chocolates you can buy. Intuition (and math) tells you that you can buy 3 chocolates. in that way, you would spend exactly 30 dollars. The key to your quick calculation was knowing that each chocolate costs 10 dollars. Congratulations! You have successfully used the power of the rate of change.
The rate of change indicates how one variable changes with respect to another. In the case of the chocolate, we notice that the price changes with respect to the number of chocolates you buy. If you buy 1 chocolate, you would spend 10 dollars, if you buy 2 the price changes to 20 dollars and so on. When the rate of change is constant then it takes a special name and it is called slopes. We also noticed that in the case of chocolate, the price depends on the number of chocolates we buy, so we call the price the dependent variable and the number of chocolates the independent variable.
Mathematically we can represent the rate of change of price with respect to a number of chocolates like this:
![\[m= \frac{10 \text{ dollars}}{\text{chocolate}}; \text{ where m is the rate of change or slope}\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-1750e5afe63e2fa98c03bc4f8d93ed46_l3.png "Rendered by QuickLaTeX.com")
Notice how the dependent variable is in the numerator and the independent variable is in the denominator. We can use slopes not only for chocolate but for many other things. Some examples are:
![\[m_{1}=\frac{2 \text{ miles}}{2 \text{ hours}} \quad m_{2}=\frac{1 \text{ cup of water}}{3 \text{ cups of flour}} \quad m_{3}=\frac{-10 \text{ customers }}{ 1 \text{ dollar increased}}\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-aff12b907da477abf490aea92543c053_l3.png "Rendered by QuickLaTeX.com")
indicates that if you drive 2 hours you cover a distance of 2 miles, so in 4 hours you would cover 4 miles. 
indicates that for every 3 cups of flour you use you need to use 1 cup of water, so if you are using 9 cups of flour then you will need 3 cups of water. 
shows that if you increase your price by 1 dollar you will lose 10 customers, so if you increase your price by 10 dollars, you would lose 100 customers.
Notice that even knowing , it is not clear how many cups of water you would need if you use 2 cups of flour. This is because the denominator is given in terms of 3 cups of flour and not in terms of 1 cup. Therefore, sometimes it is useful to represent the slope having denominator one, this gives the change per unit. Let’s see how our previous examples look if we represent them with denominator one.
![\[m_{1}=\frac{1 \text{ mile}}{ \text{ hour}} \quad m_{2}=\frac{0.333... \text{ cups of water}}{ \text{ cup of flour}} \quad m_{3}=\frac{-10 \text{ customers }}{ \text{ dollar increased}}\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-1138f1b6f20273dfb29cb56ad8b9f651_l3.png "Rendered by QuickLaTeX.com")
Notice that now we can easily see that tells us that for 2 cups of flour, we need 0.666.. cups of water.
How is the slope related to lines?
Let’s come back to the chocolate example. Can you know how much will it cost you (dependent variable) to buy 5 chocolates (independent variable) if you know the slope is 
? We have answered this question before, but let’s formalize the process.
So the cost is 50 dollars. This should look really familiar. If I replace the cost (dependent variable) with a 
, slope with an 
, and number of chocolates (independent variable) with an 
, the relationship can be written as:
![\[y=mx\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-ab159b61d2d1fa00ad30c898a5477442_l3.png "Rendered by QuickLaTeX.com")
When the slope is constant and and can be written in this way, we would say is proportional to . The graph of this proportional relation will be a line that passes through the point 
. Let’s see an example in a graph (Created using Desmos).
Let’s see what happens when we change the value of the slope. Please press the play button next to the m in the following graph.
Notice that the bigger the slope, the more steep the line is. The opposite is true if the slope approaches zero. When the slope is positive, as becomes bigger becomes bigger. When the slope is negative, as increases decreases.
From knowing just the slope you can learn a lot about how your line will look.
Finally, for the sake of completeness, let’s consider the following example. Imagine now that when you go to the store for chocolate your mom said you must buy some milk first and the rest you can spend it on chocolate. Milk costs 20 dollars (an expensive milk!). If we buy one chocolate our cost will be 10 dollars for the chocolate and 20 dollars for the milk. The total would be 30 dollars. If we buy 3 chocolates the cost will be 30 dollars for 3 chocolates and 20 dollars for the milk to a total of 50 dollars. In general;
Where 
is the cost of the milk that is always present. If you buy zero chocolates you will still need to pay dollars for the milk.
is known as the -intercept as it is the value would take if is zero. Therefore, it is the point where the line touches the -axis. Moreover, any line can be written as:
![\[y=mx+b\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-b2cf14624e392933909f61673351ab22_l3.png "Rendered by QuickLaTeX.com")
This equation is so important that it has its own name. It is called the equation of a line or slope-intercept form.
How to calculate the slope of a line
To calculate the slope of a line we rely on the information we know from the line.
Equation of the slope given two points
If you know two points 
that belong to a line, you can use the formula for slope given two points to calculate the slope:
![\[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]](https://schooltutoring.com/help/wp-content/ql-cache/quicklatex.com-6897084bfbb27a48cf995485942e95ab_l3.png "Rendered by QuickLaTeX.com")
To make sense of this formula remember that the slope is the rate of change between two variables and that the dependent variable goes in the numerator. Then you can see that the numerator is calculating the change in the dependent variable when you go from 
to 
. This is given by 
and is called the rise of our line.
Similarly, the independent variable goes in the denominator and our formula calculates the change in the independent variable when you go from 
to 
. This is given by 
and is called the run of our line.
By dividing rise over run, you obtain how much has changed as a function of and therefore you have successfully calculated the slope.
Example:
Calculate the slope of a line that passes through the points 
and 
.
Since we have two points we can use the the formula for slope given two points to calculate the slope. Choosing as 
and 
as 
(1) 
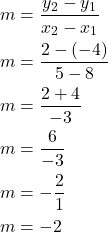
We highlight a couple of things. First, it does not matter which point you choose to be or ; the formula will work anyway. However, what is important is that once you have made your choice you do not change it. You must have and in the correct places indicated by the formula otherwise you will get the wrong answer.
Calculating the slope given a graph
If you are given the graph of a line, you can calculate the slope using the same technique that we described above.
You first need to choose two points. They can be any points. Since you have the freedom to choose the points you’ll use, you should choose wisely and try (if possible) to choose points that have exact integer values.
After that, you can use the slope formula from before and find the slope of the line using the points.
Let’s see an example using Desmos:
This has been a brief introduction to the concepts of slopes. For more information on this topic as well as assistance with homework and test preparation, feel free to reach out to an Academic Director toll-free at 1 (877) 545-7737 or via our Contact Us page.
Powered by WordPress with QuickLaTeX
