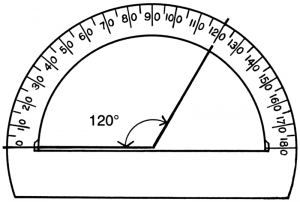
We’ve seen how to measure angles in degrees using a protractor:
However, the degree is a fairly arbitrary unit of measurement – who decided to divide the circle into 360 parts? Why can’t the circle be divided into 100 parts? 1000 parts?
Radian measure is an alternative way to measure angles. Instead of dividing the circle into an arbitrary number of parts, we look at the length of the arc that subtends the angle. We measure the angle based on this length as a ratio to the radius.
One radian is defined as the angle where the length of the arc equals the length of the radius. If we traverse the circle completely, we’ll have travelled the length of the circumference.
C = 2πr
Using this, we can find the number of radians in a circle. The length of the circumference, as a ratio to the radius, is:
# of radians in a circle = arc length /radius
Applying this to a circle, if we rearrange this equation to isolate radians, we can find the number of radians in a given number of degrees:
radians = 360 degrees / 2π
= 180 / π degrees
Rearrange to obtain:
degrees = π/180 radians
Using this formula, we can find the number of degrees in a given number of radians. To summarize, radian measure is an alternative way to measure angles. Instead of dividing the circle into an arbitrary number of parts, we look at the length of the arc that subtends the angle. We measure the angle based on this length as a ratio to the radius.
We can convert between radian and degree measure using the relationship that 2π radians equals 360 degrees; they both measure the angles in a circle:
2π radians=360 degrees