Fractions

  • Teaching Staff
  • No Comments

How to Multiply Fractions
How to Multiply Fractions 618 269 Teaching Staff

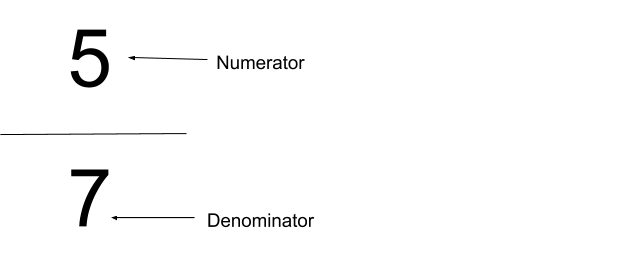
The first step to multiplying fractions is understanding the difference between the numerator and the denominator. The numerator is the top number of the fraction and the bottom number is…

read more
  • Teaching Staff
  • No Comments

Adding and Subtracting Fractions
Adding and Subtracting Fractions 2000 1520 Teaching Staff

Fractions are a very important part of math, and the first step to becoming comfortable with fractions is learning how to add and subtract them. Learning how to use fractions…

read more
  • Teaching Staff
  • No Comments

Fractions: Adding, Subtracting, Multiplying, and Dividing
Fractions: Adding, Subtracting, Multiplying, and Dividing 360 236 Teaching Staff

                                                           …

read more
  • Deborah
  • No Comments

Back to School Review of Equality and Inequality of Fractions
Back to School Review of Equality and Inequality of Fractions 150 150 Deborah

Overview The concept of dividing a whole into parts and then dividing the parts into smaller entities is basic to mathematics. That model of division can be illustrated by manipulatives…

read more
  • Deborah
  • No Comments

Math Review of Complex Rational Expressions
Math Review of Complex Rational Expressions 150 150 Deborah

Overview A complex rational expression contains a fraction within a fraction. In math language, it is a rational expression that has one or more rational expressions contained within the numerator,…

read more
  • Deborah
  • No Comments

Math Review of Least Common Multiples and Denominators in Rational Expressions
Math Review of Least Common Multiples and Denominators in Rational Expressions 150 150 Deborah

Overview Rational expressions are like fractions, and must have common denominators in order to be added or subtracted.  In order to find the smallest denominator in common, the least common…

read more
  • Deborah
  • No Comments

Math Review of Multiplying Fractions and Rates
Math Review of Multiplying Fractions and Rates 150 150 Deborah

Overview Multiplication of fractions and rates with variables is similar to multiplying regular fractions and rates. It is important to cancel out common factors and units. The General Pattern The…

read more
  • Deborah
  • No Comments

Math Review of Fractions, Decimals, and Percents
Math Review of Fractions, Decimals, and Percents 150 150 Deborah

Overview: Fractions can be converted to corresponding decimals, and both fractions and decimals can also be converted to percents.  As with many equivalent expressions in mathematics, fractions, decimals, and percents…

read more
  • Deborah
  • No Comments

Math Review of Adding and Subtracting Fractions
Math Review of Adding and Subtracting Fractions 150 150 Deborah

Overview: Adding and subtracting fractions is similar to adding and subtracting whole numbers, with one important difference.  The denominators must be the same, so that if the fractions do not…

read more
  • Deborah
  • 1,417 Comments

Math Review: Equality and Inequality of Fractions
Math Review: Equality and Inequality of Fractions 150 150 Deborah

Overview: What Are Fractions? Fractions consist of a numerator, a, and a denominator, b, so that the fraction takes the form a/b.  The denominator is the number of equal parts in…

read more
Enter your
text here