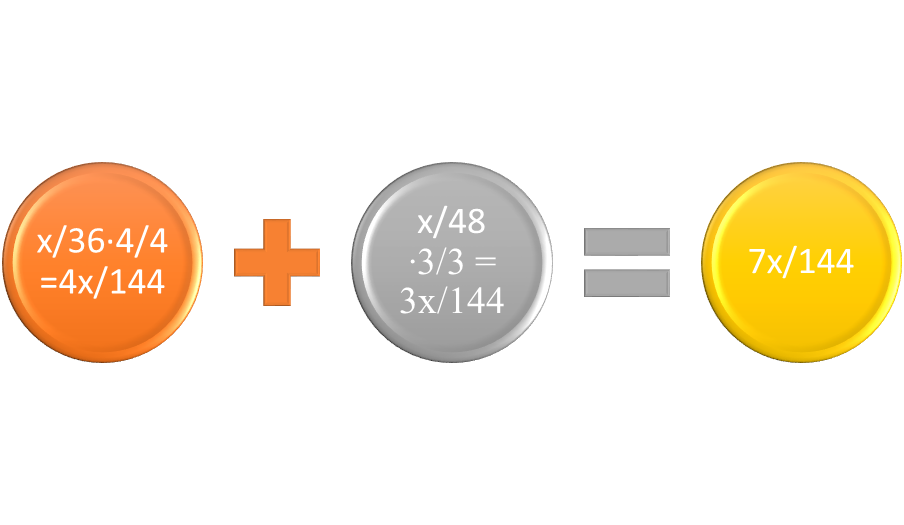Overview
Rational expressions are like fractions, and must have common denominators in order to be added or subtracted. In order to find the smallest denominator in common, the least common multiple should be found between the denominators. The least common multiple can also be calculated when the denominators are algebraic expressions.
Least Common Multiple
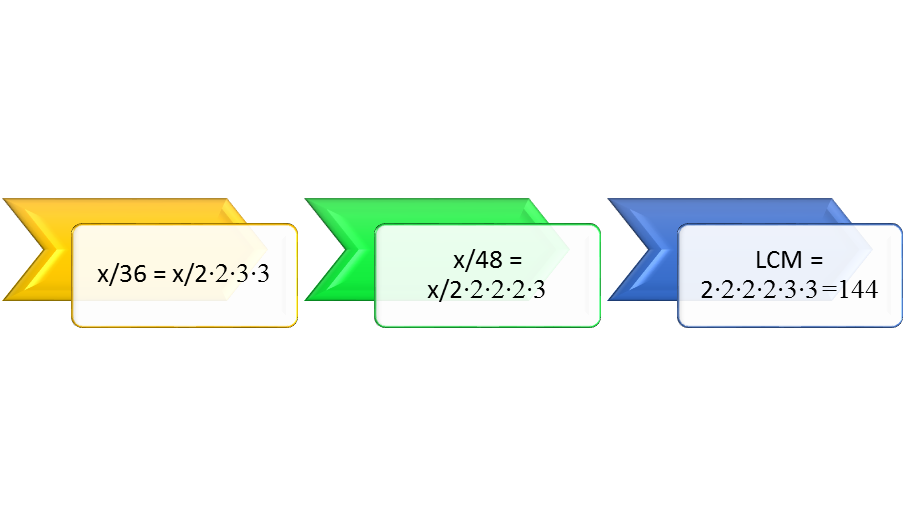
The least common multiple for rational expressions is found in two steps. Factor the denominators in the rational expressions to be added or subtracted. The least common multiple will be the factors that both denominators have in common times the factors that are not in common. Suppose the rational expressions to be added are x/36 and x/48. The constant 36 can be factored as 2∙2∙3∙3. The constant 48 can be factored as 2∙2∙2∙2∙3. The factors that 36 and 48 have in common are 2∙2∙3. The factors that they do not have in common are an additional 2.2.3. The least common multiple is 2∙2∙2∙2∙3∙3, or 144. To check, 144/36 is 4 and 144/48 is 3.
Figure 1: The least common multiple (LCM) contains the factors in common and the factors not in common.
Finding the Numerator
Before the expressions can be added, both rational expressions must be changed to their equivalents with the common denominator as the least common multiple. Using the example, x/36 is multiplied by 4/4 as 4x/144 and x/48 is multiplied by 3/3 as 3x/144. Then they can be added as rational expressions with common denominators.
Adding the Expressions
Still using the example, 4x/144 + 3x/144 equals 7x/144. The expression is already in simplest terms, because neither 7 nor x are factors of 144. Suppose x equaled 2. Then, the first fraction would be 8/144 and the second fraction would be 6/144, or 14/144. The fraction 14/144 can be simplified to 7/72. Suppose x equaled 5. Then the first fraction would be 20/144 and the second fraction would be 15/144. Adding them together would be 35/144, which would be in simplest terms.
Figure 2: To add rational expressions, each expression must have the same denominator.
LCM of Algebraic Expressions
Finding the least common multiple when algebraic expressions are in the denominators of rational expressions is a similar process to finding the least common multiple for fractions with a constant in the denominator. Suppose that the denominator of one expression is (x2 – 49) and the denominator of another expression is (x2 + 14x + 49). The expression (x2 – 49) can be factored as (x + 7)(x – 7). The expression (x2 + 14x + 49) can be factored as (x + 7)(x + 7). The factor each expression has in common is (x + 7). The factors they do not have in common are (x + 7)(x – 7). The least common denominator would be (x + 7)(x + 7)(x – 7).
Figure 3: To calculate the LCM, factor algebraic expressions for the common factors and the factors not in common.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Buckeye, AZ: visit Tutoring in Buckeye, AZ