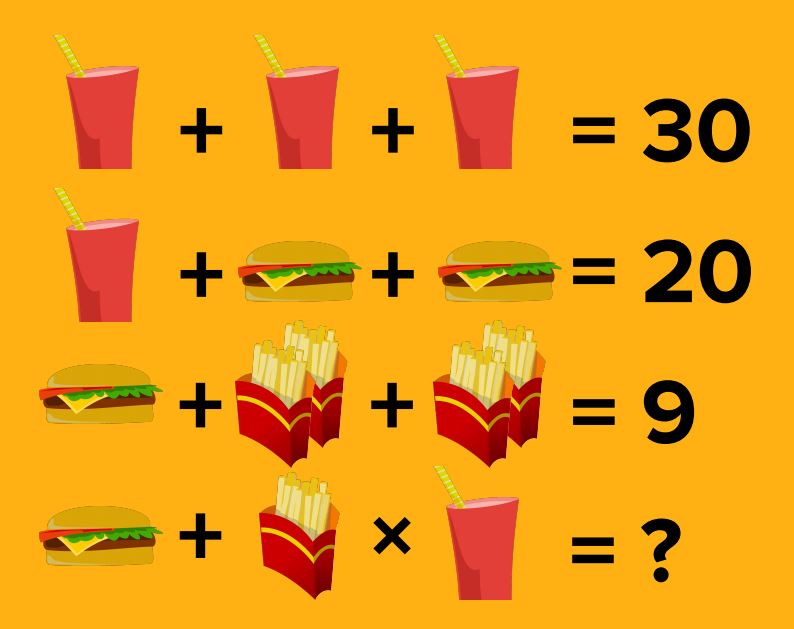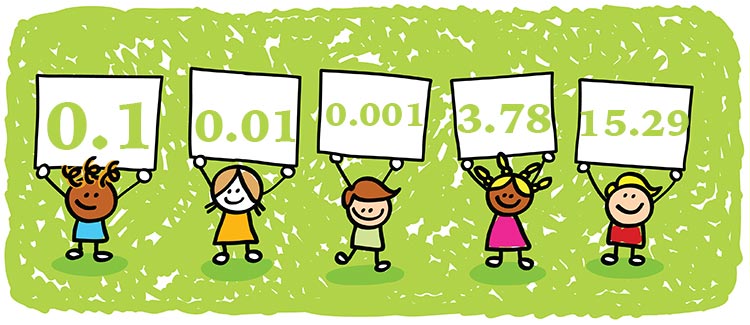Login Get started

Formulae and Equations

  • joshua
  • No Comments

Proving and Using the Pythagorean Theorem
Proving and Using the Pythagorean Theorem 589 281 joshua
Here we will look at one of the most important equations in geometry: the Pythagorean Theorem. We will begin by defining the Pythagorean Theorem and then we will demonstrate a short proof. Finally, we will look at two examples of how we might use the the Pythagorean Theorem in a real-world context. read more
  • joshua
  • No Comments

Finding Asymptotes and Holes of Rational Functions
Finding Asymptotes and Holes of Rational Functions 640 480 joshua
Here we will be looking at some defining features of rational functions: asymptotes and holes. We will begin by defining rational functions,. We will then proceed to uncover how to identify different types of asymptotes and how to distinguish them from holes. In each case, we will use example functions to visualize the effects and representations of these features. read more
  • Teaching Staff
  • No Comments

Tips for Factoring Polynomials
Tips for Factoring Polynomials 970 1024 Teaching Staff

Polynomial Factoring:   As in many fields, the manner in which we approach a problem In mathematics can greatly affect how we go about solving it. By finding the factors…

read more
  • Teaching Staff
  • No Comments

Le Châtelier’s Principal
Le Châtelier’s Principal 656 720 Teaching Staff

A difficult concept in chemistry is the equilibrium of chemical equations. Chemical reactions do not always react to completion, and they can proceed in either direction if it is written…

read more
  • Teaching Staff
  • No Comments

The Pythagorean Theorem
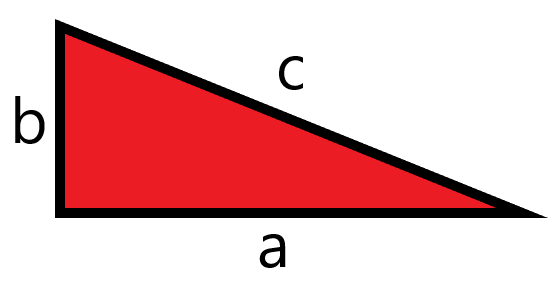
The Pythagorean Theorem 960 664 Teaching Staff

Triangles are an important shape that come up all over the place in life, which is why trigonometry is one of the most important fields of mathematics. Pythagorean theorem is…

read more
  • Teaching Staff
  • No Comments

Population Genetics: The Hardy-Weinberg Equilibrium
Population Genetics: The Hardy-Weinberg Equilibrium 960 640 Teaching Staff

The Hardy-Weinberg equilibrium is a model that proposes allele (variations of a gene) and genotype (genetic makeup) frequencies within a population remain constant when the population is in equilibrium. If…

read more
  • Teaching Staff
  • No Comments

Adding and Subtracting Fractions
Adding and Subtracting Fractions 2000 1520 Teaching Staff

Fractions are a very important part of math, and the first step to becoming comfortable with fractions is learning how to add and subtract them. Learning how to use fractions…

read more
  • Teaching Staff
  • No Comments

Solving a System of Equations: Substitution and Elimination
Solving a System of Equations: Substitution and Elimination 794 629 Teaching Staff

When dealing with a system of linear equations there are two methods to algebraically solve the question. One is substitution and the other is elimination which is meant to be…

read more
  • Teaching Staff
  • No Comments

Multiplying and Dividing Decimals
Multiplying and Dividing Decimals 750 325 Teaching Staff

Multiplying and dividing is a very important and fundamental math skill that every student should have down. However, problems that many encounter in real and not all questions that are…

read more
  • Teaching Staff
  • No Comments

Taking Basic Derivatives
Taking Basic Derivatives 1024 538 Teaching Staff

Derivative: an expression that represents the rate of change of a function. At this level, it is usually denoted as y’ or f’(x) (read y prime and f prime at…

read more
Enter your
text here