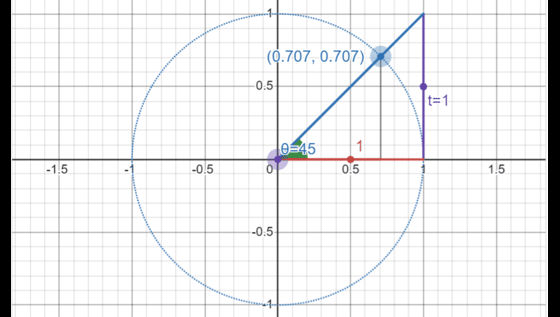
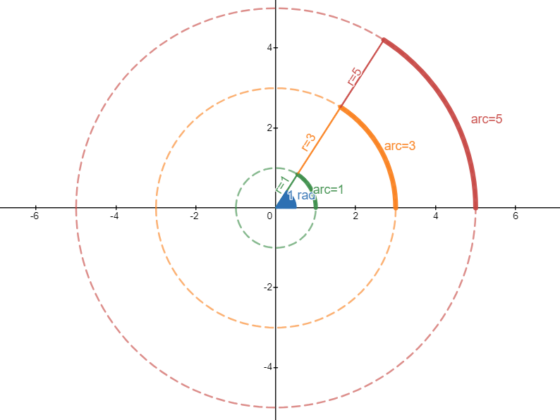
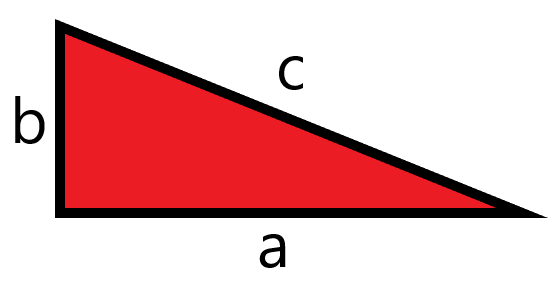
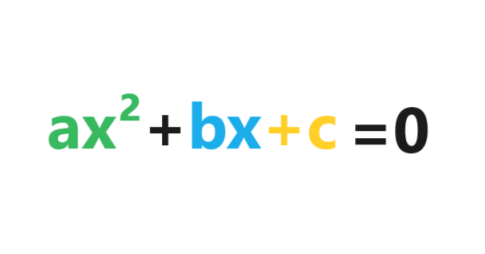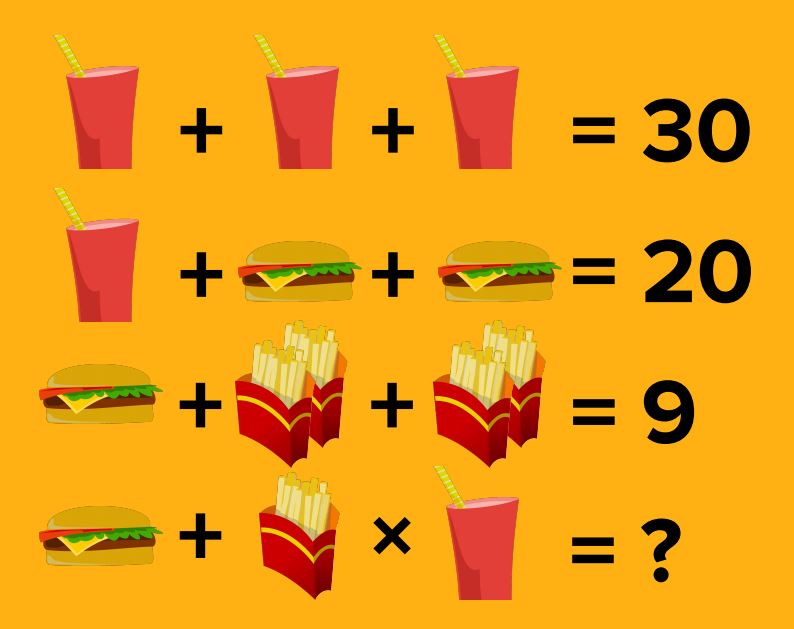Math Fundamentals

The unit circle showing the tangent of an angle as the length of the tangent line in the circle.
  • Jeff
  • No Comments

What is the Unit Circle and Why is it Important?
What is the Unit Circle and Why is it Important? 600 317 Jeff
We explore how to use the unit circle to understand some properties of trigonometric ratios and why this circle is so important in math. read more
The relationship between 1 radian and the radius of a circle
  • Jeff
  • No Comments

What are Radians and Why we Use them
What are Radians and Why we Use them 794 717 Jeff
A radian is the natural unit of angles, but why do we use them instead of degrees. In this post we discuss the relationship between angles, radians and degrees. read more
  • joshua
  • No Comments

Proving and Using the Pythagorean Theorem
Proving and Using the Pythagorean Theorem 589 281 joshua
Here we will look at one of the most important equations in geometry: the Pythagorean Theorem. We will begin by defining the Pythagorean Theorem and then we will demonstrate a short proof. Finally, we will look at two examples of how we might use the the Pythagorean Theorem in a real-world context. read more
Quadratic Equation
  • Jeff
  • No Comments

Solving Quadratic Equations
Solving Quadratic Equations 485 254 Jeff
The quadratic equation is one of the most important topics in math, but sometimes it could look a bit complicated. We explore some of the simplest methods to solve quadratic equations and offer some examples of each. read more
  • joshua
  • No Comments

Finding Asymptotes and Holes of Rational Functions
Finding Asymptotes and Holes of Rational Functions 640 480 joshua
Here we will be looking at some defining features of rational functions: asymptotes and holes. We will begin by defining rational functions,. We will then proceed to uncover how to identify different types of asymptotes and how to distinguish them from holes. In each case, we will use example functions to visualize the effects and representations of these features. read more
  • Teaching Staff
  • No Comments

Tips for Factoring Polynomials
Tips for Factoring Polynomials 970 1024 Teaching Staff

Polynomial Factoring:   As in many fields, the manner in which we approach a problem In mathematics can greatly affect how we go about solving it. By finding the factors…

read more
  • Teaching Staff
  • No Comments

Adding and Subtracting Fractions
Adding and Subtracting Fractions 2000 1520 Teaching Staff

Fractions are a very important part of math, and the first step to becoming comfortable with fractions is learning how to add and subtract them. Learning how to use fractions…

read more
  • Teaching Staff
  • No Comments

Solving a System of Equations: Substitution and Elimination
Solving a System of Equations: Substitution and Elimination 794 629 Teaching Staff

When dealing with a system of linear equations there are two methods to algebraically solve the question. One is substitution and the other is elimination which is meant to be…

read more
  • Teaching Staff
  • No Comments

Multiplying and Dividing Decimals
Multiplying and Dividing Decimals 750 325 Teaching Staff

Multiplying and dividing is a very important and fundamental math skill that every student should have down. However, problems that many encounter in real and not all questions that are…

read more
  • Teaching Staff
  • No Comments

Taking Basic Derivatives
Taking Basic Derivatives 1024 538 Teaching Staff

Derivative: an expression that represents the rate of change of a function. At this level, it is usually denoted as y’ or f’(x) (read y prime and f prime at…

read more
Enter your
text here