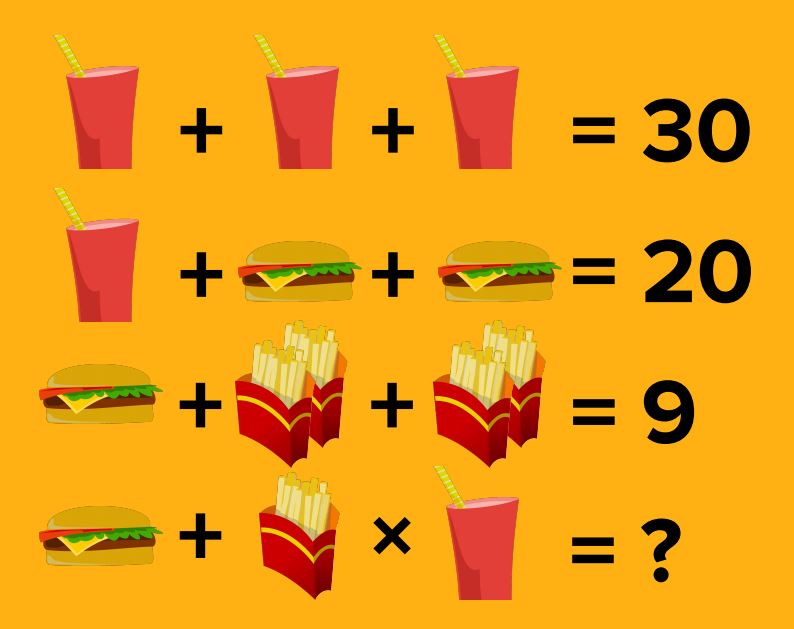Triangles are an important shape that come up all over the place in life, which is why trigonometry is one of the most important fields of mathematics. Pythagorean theorem is…
read more
Fractions are a very important part of math, and the first step to becoming comfortable with fractions is learning how to add and subtract them. Learning how to use fractions…
read more
When dealing with a system of linear equations there are two methods to algebraically solve the question. One is substitution and the other is elimination which is meant to be…
read more
Multiplying and dividing is a very important and fundamental math skill that every student should have down. However, problems that many encounter in real and not all questions that are…
read more
Definitions: A rational function is defined as a function where both the numerator and denominator are polynomials. A hole is a point where the function is undefined. An asymptote is…
read more
Overview Percents are based on the decimal system and have many useful applications in business, sales, and finance. Other applications of percents include percent increase and decrease. Estimating Percentages Many…
read more