Trigonometry

The unit circle showing the tangent of an angle as the length of the tangent line in the circle.

Jeff
March 27, 2024
No Comments

What is the Unit Circle and Why is it Important?

What is the Unit Circle and Why is it Important? https://schooltutoring.com/help/wp-content/uploads/sites/2/2024/03/unit-cicle-1-1.png 600 317 Jeff Jeff https://secure.gravatar.com/avatar/48c4c6cdb7975c0042b502b132288352?s=96&d=mm&r=g March 27, 2024 March 27, 2024

We explore how to use the unit circle to understand some properties of trigonometric ratios and why this circle is so important in math. read more

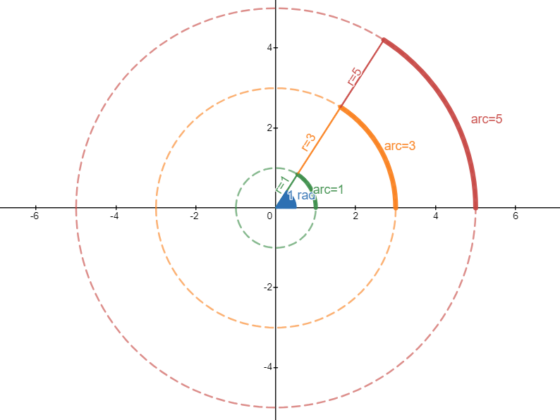
The relationship between 1 radian and the radius of a circle

Jeff
February 29, 2024
No Comments

What are Radians and Why we Use them

What are Radians and Why we Use them https://schooltutoring.com/help/wp-content/uploads/sites/2/2024/02/relation-radian-and-radius.png 794 717 Jeff Jeff https://secure.gravatar.com/avatar/48c4c6cdb7975c0042b502b132288352?s=96&d=mm&r=g February 29, 2024 February 29, 2024

A radian is the natural unit of angles, but why do we use them instead of degrees. In this post we discuss the relationship between angles, radians and degrees. read more

joshua
February 6, 2024
No Comments

Proving and Using the Pythagorean Theorem

Proving and Using the Pythagorean Theorem https://schooltutoring.com/help/wp-content/uploads/sites/2/2024/02/Right-Triangle.png 589 281 joshua joshua https://secure.gravatar.com/avatar/8bedbbb695a440e8cd1a2d334ddeb54c?s=96&d=mm&r=g February 6, 2024 February 6, 2024

Here we will look at one of the most important equations in geometry: the Pythagorean Theorem. We will begin by defining the Pythagorean Theorem and then we will demonstrate a short proof. Finally, we will look at two examples of how we might use the the Pythagorean Theorem in a real-world context. read more

Teaching Staff
March 21, 2019
No Comments

The Pythagorean Theorem

The Pythagorean Theorem https://schooltutoring.com/help/wp-content/uploads/sites/2/2019/03/blackboard-1644744_960_720.png 960 664 Teaching Staff Teaching Staff https://secure.gravatar.com/avatar/d96b825901af08f4b20fdfa2d056868f?s=96&d=mm&r=g March 21, 2019 March 21, 2019

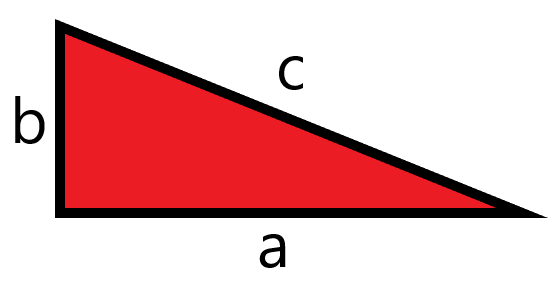
Triangles are an important shape that come up all over the place in life, which is why trigonometry is one of the most important fields of mathematics. Pythagorean theorem is…

Teaching Staff
July 12, 2018
No Comments

Working with Log

Working with Log https://schooltutoring.com/help/wp-content/uploads/sites/2/2018/07/cf0338d495d6c8a1c40d4a1e5b8eb859.jpg 2100 1500 Teaching Staff Teaching Staff https://secure.gravatar.com/avatar/d96b825901af08f4b20fdfa2d056868f?s=96&d=mm&r=g July 12, 2018 July 12, 2018

…

Teaching Staff
July 10, 2018
No Comments

Proving (or Disproving) Triangles are Similar

Proving (or Disproving) Triangles are Similar https://schooltutoring.com/help/wp-content/uploads/sites/2/2018/07/kvefr0506s.jpg 660 440 Teaching Staff Teaching Staff https://secure.gravatar.com/avatar/d96b825901af08f4b20fdfa2d056868f?s=96&d=mm&r=g July 10, 2018 July 10, 2018

Definition: Similar triangles have equal corresponding angles and proportional sides. There are three main methods to prove triangles are similar. The information provided in the question dictates which approach…

Deborah
January 14, 2015
No Comments

Math Review of Trigonometry and Navigation

Math Review of Trigonometry and Navigation https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 Deborah Deborah https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=mm&r=g January 14, 2015 January 14, 2015

Overview Trigonometry in the form of triangulation is at the heart of navigation, whether it is by land, sea, or air. GPS systems use triangulation to find and fix positions,…

Deborah
January 5, 2015
No Comments

The Measurement of Parallax: Angles We Have Seen on High

The Measurement of Parallax: Angles We Have Seen on High https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 Deborah Deborah https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=mm&r=g January 5, 2015 January 5, 2015

Overview The demonstration of parallax is as close as an observer’s own two eyes. It is the measurement of how the same object appears from two different points of view.…

Deborah
December 18, 2014
No Comments

Math Review of Platonic Solids and Polyhedra

Math Review of Platonic Solids and Polyhedra https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 Deborah Deborah https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=mm&r=g December 18, 2014 December 18, 2014

Overview There are infinitely many regular polygons. However, there are a fixed number of regular polyhedra, called Platonic solids. Mathematicians use the definitions of the regular polygons and the characteristics…

Deborah
December 17, 2014
No Comments

Math Review of More Properties of Circular Functions

Math Review of More Properties of Circular Functions https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 Deborah Deborah https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=mm&r=g December 17, 2014 December 17, 2014

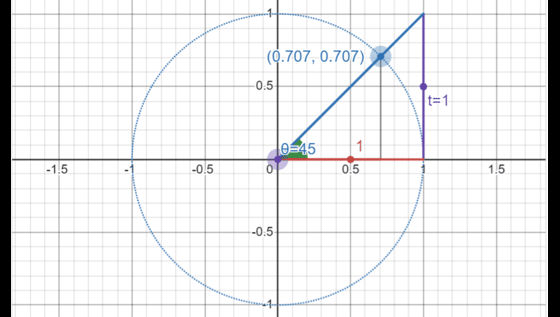
Overview The unit circle has as its center the origin point of the Cartesian coordinates x and y, and has a radius 1. The trigonometric functions are also called circular…

What is the Unit Circle and Why is it Important?

What are Radians and Why we Use them

Proving and Using the Pythagorean Theorem

The Pythagorean Theorem

Working with Log

Proving (or Disproving) Triangles are Similar

Math Review of Trigonometry and Navigation

The Measurement of Parallax: Angles We Have Seen on High

Math Review of Platonic Solids and Polyhedra

Math Review of More Properties of Circular Functions

Home Tutoring

Specialized Programs

By Grade

By Subject

Getting Started

Help and Contact