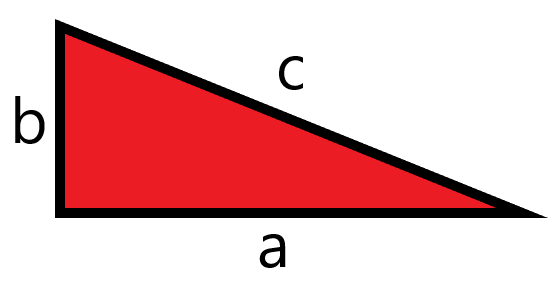
Years ago, a mathematician namely Pythagoras stated a theorem on right angles triangles. Hence the theorem is named as Pythagoras theorem. Pythagoras theorem states that “In a right angled triangle, the square of length of the hypotenuse (the longest side) is the sum of the squares of the other two sides.
By Pythagoras theorem,
c2 = a2+b2
where c is the hypotenuse and a,b are the legs of the right angle triangle.
This means that, if we frame the squares along all the three sides of a right angled triangle then the area of square along hypotenuse is equal to the areas of the other two squares put together.
Example:
Here 52 = 32 + 42
25 = 9+16
25=25.
So, Pythagoras theorem is used to determine whether the given triangle is right-angled.
Since here we got 25=25 using the statement of Pythagoras theorem, we can say that the triangle with lengths 3,4 and 5 is right-angled.
Also, Pythagoras theorem is used to determine the length of an unknown side of a right angled triangle.
Example:
By Pythagoras theorem,
a2 + 42 = 52
a2 + 16 = 25
a2 = 25-16=9
a = √9=3
In the same way, Pythagoras theorem is used to obtain the formula for the diagonal of a square.
Since all the angles in square are right angles, Pythagoras theorem can be applicable for the triangle which is inside the square.
So, diagonal2 = a2 +a2=2a2
So, the diagonal of square = √2 a
Still need help with Mathematics? Please read more about our Mathematics tutoring services.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Newman visit: Tutoring in Newman.