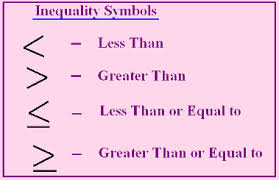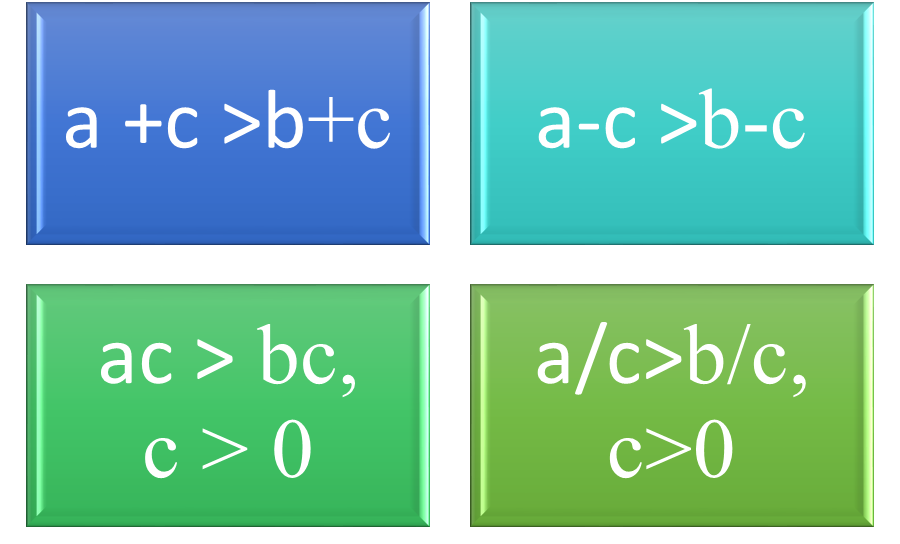Overview
While equations are statements that two quantities are equal, inequalities state that quantities are not equal. One side of the expression might be greater than the other side, or one side of the expression may be less. Correct solutions for variables encompass more than one number.
Inequalities
Inequalities include symbols such as greater than >, less than <, greater than or equal to ≥, less than or equal to ≤, or not equal to ≠. They can be expressed in words such as the real numbers that are greater than 5, in symbols such as x >5, or in set builder notation {x| x>5}. The values that solve the inequality are those that make it true. If x>5, then 4 cannot be a solution, but 5.01 can be. Similarly, if y +3 >5, then 3 can be a solution, because 3 +3 is 6 and 6 is greater than 5.
Graphing Inequalities
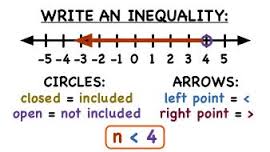
Writing a solution set in set-builder notation and listing enough members to give the pattern can consume both time and space. For example, the solution to {z | z -3 <12} can include {15.1, 15.2, 15.3, 15.4 …16, 16.1, 16.2 …} and so on. It can also be graphed on the number line. If the inequality is stated as either greater than or less than, than the endpoint of the ray is not a solution and it can be left as an open circle. If the variable is isolated on the left side of the inequality symbol, then the graph on the number line can point in the same direction as the inequality symbol. For example, 3 > x can be rewritten as x <3, and all numbers on the number line are less than 3 can be shaded in the same direction.
Solving Inequalities by Adding or Subtracting
Solving inequalities uses the same identity properties for addition and subtraction as solving equations. For example, to solve an inequality such as 3 + x <12, use the additive inverse so that 3-3 +x <12 -3. That isolates the variable, so x <9. Suppose that q – ½ >6. Then q- ½ + ½ > 6 + ½.
Solving Inequalities by Multiplying or Dividing
Solving inequalities by multiplying or dividing uses the same identity properties as equations with one important difference. If the number to be multiplied or divided is positive, then the direction of the inequality stays the same. However, if the number to be multiplied or divided is negative, the direction of the inequality is reversed.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Sitka, AK: visit: Tutoring in Sitka, AK