Overview
Systems of inequalities can be solved in much the same way as linear equations. If there is a solution in which the systems intersect, it will be in terms of a plane figure rather than a single point.
Review of Inequalities
Suppose the inequality is in the form x +y >2. The solution set will consist of all values for x and y that are greater than 2; for example, the value (3, 2). The graph for that solution set would include all points above but not including the line x + y = 2. If the inequality were x + y ≥ 2, the graph would include the line for x + y = 2. Similarly, if the inequality were x +y <2, the solution set would consist of all values of x and y that are less than 2; for example (0, 1). The graph for the solution set would include all values that were below the line x + y = 2.
Systems of Inequalities
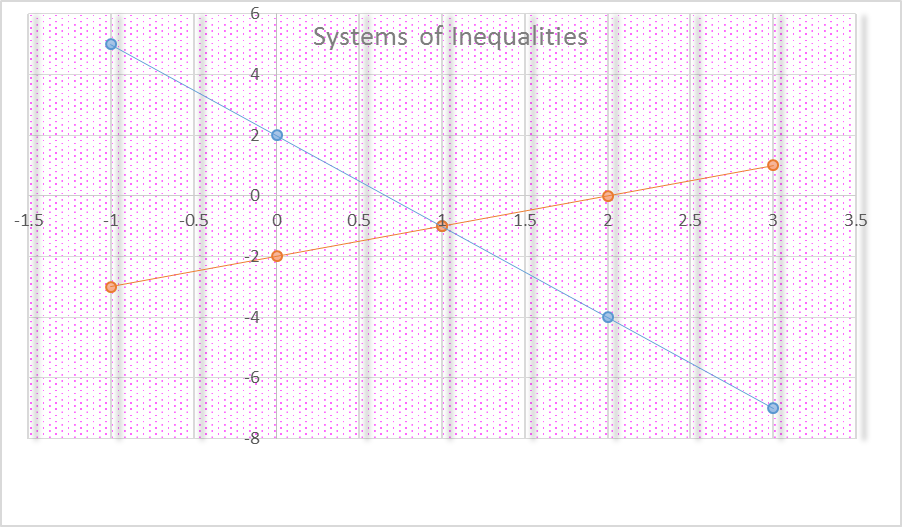
Solving systems of inequalities is similar to solving systems of equations. Suppose the problem were to find the common solutions for y ≥ -3x + 2 and y< x – 2. It could be solved by any of the methods to solve systems of equations, by addition, substitution, or multiplication. Both the equations go through the point (1, -1), as -1 = -3 + 2, and -1 = 1 – 2. The graph for the solution set of y≥-3x + 2 would consist of all points above the line and including the line, and the graph for the solution set y < x – 2 would consist of all points below the line y < x – 2. The intersection of those plane figures would consist of all points that include both inequalities.
Figure 1: The solution is represented by the points within the angle with vertex (1, -1) where x is greater than 1 and y is less than -1
Inequalities as Quadrants
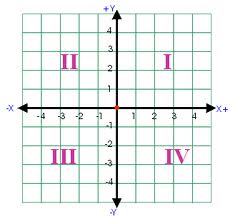
Another way to think of systems of inequalities is when the solution set for an inequality represents an entire quadrant or most of a quadrant on a coordinate plane. Suppose x> 0 and y>0. If x >0, then y can be any value, so all the points to the right of the x axis will be in the solution. However, if y is also greater than 0, then only the points in the upper right quadrant will be included (Quadrant I). Similarly, if x is greater than 0 and y is less than 0, only the points in the lower right quadrant will be included (Quadrant III). If x is less than 0 and y is greater than 0, only the points in the upper left quadrant will be included (Quadrant II). If x is less than 0 and y is also less than 0 then the points in the lower left quadrant will be included (Quadrant IV).
Figure 2: Representation of the coordinate plane.
Geometric Representations
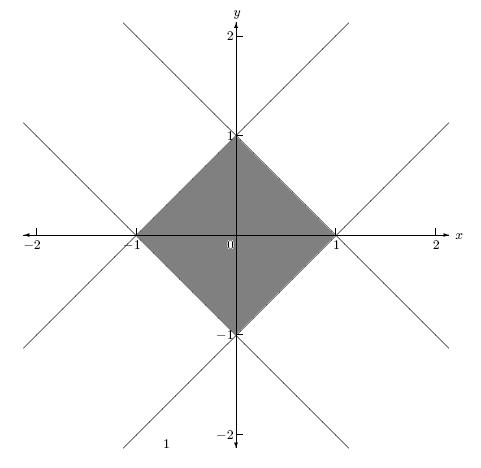
The solutions of systems of inequalities can be represented as plane figures, because there are infinitely many points that are contained within any geometric figure. Even if all points cannot be listed, they can be described. For example, the solution set of inequalities y ≥ -3x+2 and y< x-2 is an angle with vertex at (1, -1). Similarly, the solution set of x>0, y>0, x +y <75 and x +y >50 can be described in terms of the geometric figure it represents.
Figure 3: A geometric figure represents infinitely many points on a coordinate plane.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Grapevine, TX: visit Tutoring in Grapevine, TX