Overview
Many quadratic equations can be solved by a process called “completing the square.” The process uses the definitions of square roots, as well as the principles of adding or subtracting constants.
Equations in the Form ax2 = p
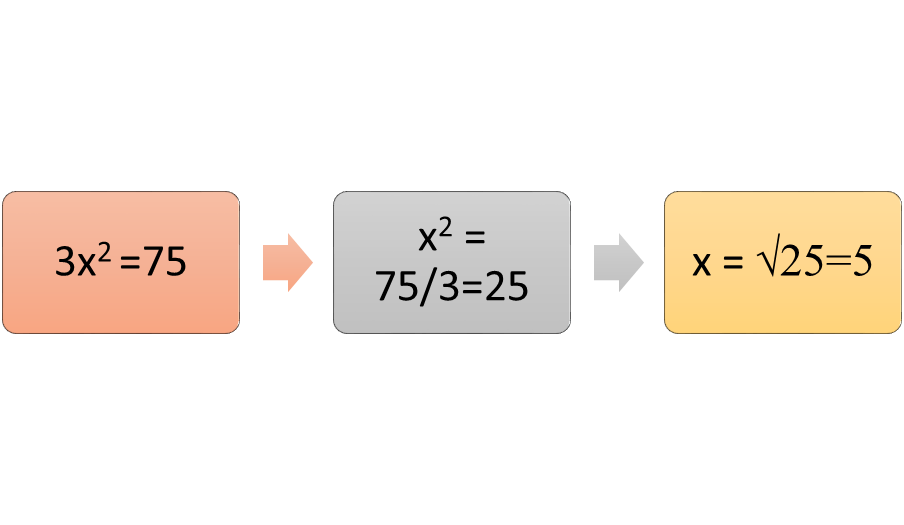
Equations in the form ax2 = p are quadratic equations. Suppose the coefficient a is equal to 1, so that the equation is x2 = p (and p is greater than 0, so that the problem has a real-number solution). The value of x will equal the square root of p, or √p, using the radical). For example, if x2 = 144, then x = 12, the square root of 144. Using the definition of square roots, there are 2 square roots of 144, 12, and -12, because 12∙12 = 144, and -12∙-12 also equals 144. An easier way in symbol form is that √144 = ±12. If the coefficient a is greater than 1, then the value of x will equal ±√p/a. For example, suppose 3x2 = 75. Then x ± √75/3, or x ±5.
Figure 1: Solving for x when x is squared
Equations in the Form (x + c)2 = d
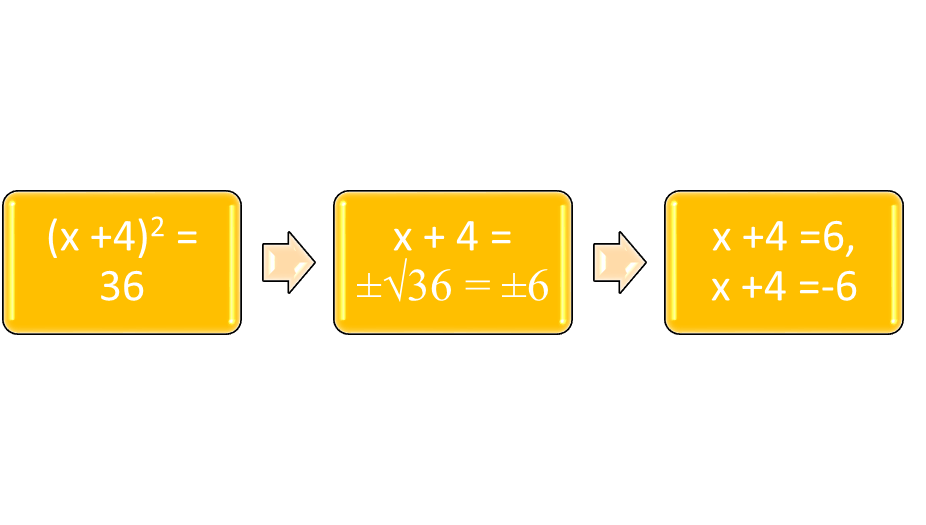
Equations in the form (x + c)2 = d are also quadratic equations in the form of perfect square trinomials. The simplest way to solve them is by using the definition of square roots. Suppose that (x + 4)2 = 36. Then, by the definition of square roots, x + 4 ± 6. If 6 is positive, then x equals 2, but if 6 is negative, then x = -10. Suppose that the perfect square trinomial were expanded so that x2 + 8x + 16 = 36. The solutions for x would still be 2 and -10, because if x = 2, then 4 + 16 + 16 = 36. Similarly, 100 – 80 + 16 = 36.
Figure 2: Use the definition of square roots to solve perfect square trinomials.
Completing the Square
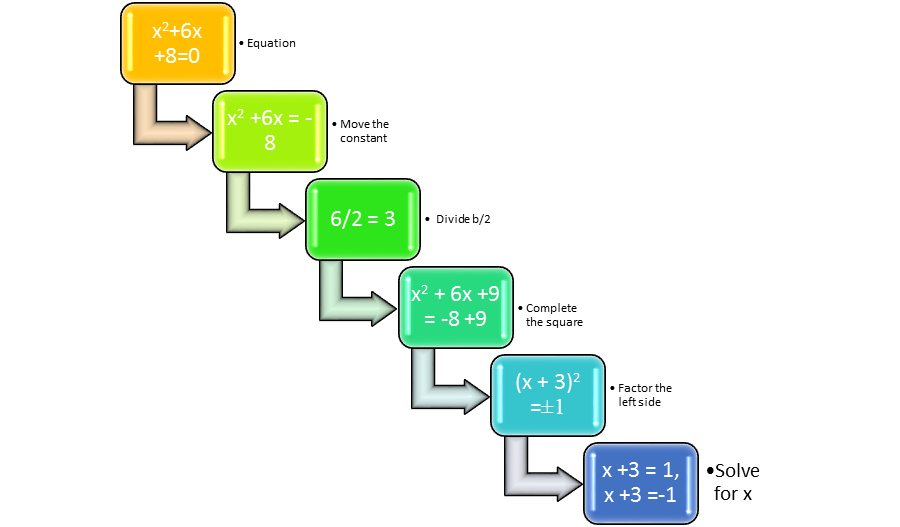
Suppose the equation were x2 + 6x + 8 = 0. It is not a perfect square trinomial like x2 + 8x + 16. When the coefficient for the x2 term is 1, half of the b coefficient (for the x term) is squared to form the c coefficient. In the perfect square trinomial x2 + 8x + 16, for example, half of 8 is 4, and 42 is 16. That property, as well as addition rules in algebra, can be used to complete the square. The first step is to turn the equation into a form that can be used to complete the square by moving the c term to the other side of the equation. This turns x2 + 6x + 8 = 0 to x2 + 6x = -8, by subtracting 8 from both sides. If the equation were a perfect square trinomial, half of the b coefficient would be squared to form the c coefficient. The b coefficient in this equation is 6, and half of 6 is 3. The c term is 32 or 9. Using the addition rules of algebra, 9 can be added to both sides of the equation to form x2 + 6x +9 = -8 +9. Factoring the left side of the equation, (x + 3)2 = 1. Therefore, x +3 =±√1. It is very important to remember that a number has a positive and a negative square root in order to solve both values of x. If the square root of x is positive, then x + 3 = 1, so x = -2. If the square root of x is negative, then x + 3 = -1, so x = -4.
Figure 3: The path to completing a square.
Geometric Representation of Completing the Square
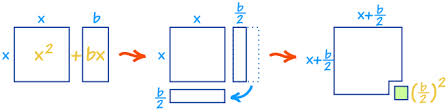
Another way of looking at completing the square is by looking at the geometric representation of how a square is completed. The equation x2 + bx = a (which is the same equation as when the c term is moved), can be seen as a geometric figure that consists of a square with sides x and two rectangles with sides bx. The “missing piece” that is completed is a square that has both sides equal to b/2.
Figure 4: Another way to look at completing the square.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Nanaimo, BC, Canada: visit Tutoring in Nanaimo, BC, Canada